Skip over navigation
Here's a picture of a set of steps and a ladder.
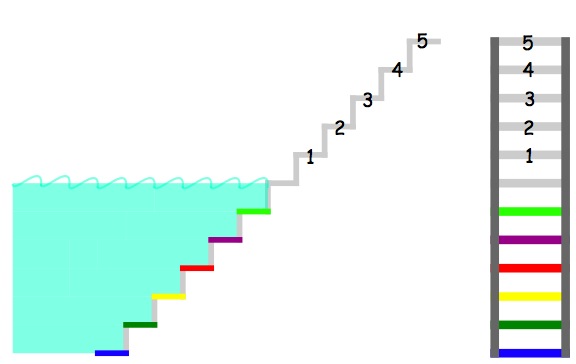
You'll probably notice that I've coloured the steps.
The first step into the water is light green, the second step is purple, the third red and so on.
The same is true of the ladder.
Later, I'll be thinking about numbering these coloured steps.
1. Suppose your friend puts you on step $4$ and you only want to go a little way into the water so you head for the red step. Stepping down carefully, one step at a time, how many steps will you have to take?
2. Now the next time you want to go into the water your friend takes you to step $2$ and you're going to step down carefully to the blue step at the bottom. How many steps down do you have to take?
3. When you have finished swimming you take yourself to the yellow step and meet your friend on step $5$. How many steps, one at a time, do you have to take?
Maybe it's time to number these coloured steps.
I think I'll go for numbering them down from the water surface.
Can you invent your own way of numbering the steps which go under the water?
Swimming Pool
Age 5 to 11
Challenge Level 
Swimming Pool
Have you been to a swimming pool lately?
When you go swimming you might walk down some steps to reach the bottom, or you might use a ladder at the side of the pool.Here's a picture of a set of steps and a ladder.
You'll probably notice that I've coloured the steps.
The first step into the water is light green, the second step is purple, the third red and so on.
The same is true of the ladder.
Later, I'll be thinking about numbering these coloured steps.
1. Suppose your friend puts you on step $4$ and you only want to go a little way into the water so you head for the red step. Stepping down carefully, one step at a time, how many steps will you have to take?
2. Now the next time you want to go into the water your friend takes you to step $2$ and you're going to step down carefully to the blue step at the bottom. How many steps down do you have to take?
3. When you have finished swimming you take yourself to the yellow step and meet your friend on step $5$. How many steps, one at a time, do you have to take?
Maybe it's time to number these coloured steps.
I think I'll go for numbering them down from the water surface.
Can you invent your own way of numbering the steps which go under the water?
Why do this problem?
This activity can be used as a starting point for introducing, and raising children's awareness of, negative numbers.
Possible approach
The first part of the problem is effectively counting along a number line in different directions, but in this case it is vertical rather than the more usual horizontal orientation, so that we are moving up and down rather than right and left. The final part of the activity encourages children to be creative and invent their own way of numbering the steps below the water level. This will
undoubtedly provide some interesting points for discussion amongst the whole class. You may want to share a few of their ways with everyone, asking the relevant children to explain why they think their way works well. There could be some debate about which ways might work best.
At this stage, you could specifically introduce the idea of negative numbers. One way to do this is to ask children whether they know of any number scales which are vertical and this might make them think of a thermometer. It would be great to have a thermometer to hand and then you could look together at the negative parts of the scale, talking about what they mean. You could then transfer
this negative number scale to the swimming pool. At a higher level, the next stage would be to revisit the swimming pool problem here and discuss numerical differences between negative and positive numbers.
Key questions
Can you tell me about how you are working these out?
Possible extension
Some pupils could move away from the swimming pool situation and be given other situations to find the numerical difference between two numbers - one positive and one negative.
Possible support
Pupils may find it helpful to have a small vertical number line going from the negative to the positive. It may be necessary to have some discussion about the place of zero.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?