Skip over navigation
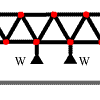
Bridge Builder
Age 16 to 18
Challenge Level 
Why use this problem
A great deal of insight into Latticework problems can be
achieved without the need for any numerical computation at all: we
rely on vector methods and the simple principles of tension and
force to determine the character of the tensions and compressions
in the bridge. The use of ropes and springs will make students
think about the difference between an internal tension and an
internal compression.
This problem will help students to realise that numerical and
algebraic manipulation are not always necessary as the first step
in a mechanics problem; it also helps to train students' self
checking mechanisms.
This problem also reinforces basic ideas concerning vectors
and components.
Possible Approach
Students will probably be tempted to try to calculate the
magnitude of all of the forces algebraically but that is
unnecessary in this question. To help reinforce this idea, you
could discuss the problem as a group, beginning with the question
of how vectors will help us in the problem.
Although students should be encouraged to solve the problem
without algebra, they may wish to perform an algebraic calculation
to convince themselves that their deductions are indeed correct.
Hopefully after some thought the principle will become clear and
'obvious' to the students.
The approach used in this question might seem unusual to many
students and could form the basis for a discussion about
mathematics. Although the question will not require any numerical
calculation, a good answer will need to be clearly and accurately
explained. Students could explain their answers to the group. Does
the group feel that the answer is robust? Are there any weaknesses
in the argument that might need clarification? Conversely, are
there any particularly clear aspects of the argument? How do
students feel about not using numbers? Are they aware that the lack
of algebra does not in any way reduce the mathematical importance
or significance of a task? Would an algebraic calculation involving
the mass of the weight make the result any more believable?
Key Questions
- What are the differences between a spring and a string?
- In order for a pin joint to experience no net forces what must be satisfied?
- How can vectors help us in this problem?
Possible Extension
Once the concept of resolution of vector components is
understood, there are several avenues of further investigation for
this problem, such as the following
- The bridge in this question is made from 7 triangular segments. What happens if the weight is hanging from the centre of a bridge with more triangular segments?
- What happens if the bridge is made from isosceles-triangular segments instead of equilateral-triangular segments?
- What would happen if an extra row of triangles were jointed onto the top of the bridge?
- Which springs/ropes would experience the most/least internal forces?
In addition, there is a follow-up extension problem to this
task: more bridge building
.
Possible Support
You could first try a simpler version of the problem in which the bridge is made from three triangular segments. What direction must the forces be pointing in the central two portions of the bridge?You may also like
Lunar Leaper
Gravity on the Moon is about 1/6th that on the Earth. A pole-vaulter 2 metres tall can clear a 5 metres pole on the Earth. How high a pole could he clear on the Moon?
Wobbler
A cone is glued to a hemisphere. When you place it on a table in what position does it come to rest?
More Bridge Building
Which parts of these framework bridges are in tension and which parts are in compression?