First Connect Three

Daisy and Izzy from Thomas Eaton Primary Academy described a similar strategy to each other. Daisy wrote:
First I tried to make the highest number I could. Then with the numbers I got I would make the closest possible answer to go near it. When ever my opponent was getting close to winning I would focus on getting in their way so they wouldn't win.
Izzy added: 
Then you need to keep an eye on the person you're playing against as they will block you. Try get three in a row but keep your options open as you may not get the numbers you wanted.

Sara from the International School of Brussels shared her work:

    click to see full size


and this came from Smilla, also from the International School of Brussels:


      click to see full size


Adam from Willowbank in New Zealand thought it was best to start in a different place:
I think it's best to try and aim for the 6 numbers in the middle 0,1,2,5,6,7 because you have a high chance of winning because it will be easy to get a diagonal horizontal or vertical 3.


Coen from Bainbridge School in the UK used a similar strategy, but for slightly different reasons:
If I was you, I would aim for the lower numbers because you have got more of a chance to win. The easiest number to get is 7 because you quite often get a 3 or a 4, but if you takeaway then you will get 1.
The minus numbers are the hardest numbers to get because you quite often get higher numbers and if you takeaway you will probably get 1, 2, 3 or 4. But if you get 5, 6 or 7 when you have rolled the dice and the other one says 5 then you could possibly get -1, -2, 0.


Louisa from Walton High School in the UK also thought about which would be the easiest and hardest numbers to get:
The hardest numbers to get are -5 and 12 because for both of them there is only one combination of numbers which you can roll to get them as a total.


Daniella, Sandra and Michelle from Park Lane International School in the Czech Republic worked out how many ways there are of making each number, and how many lines there are through each number:
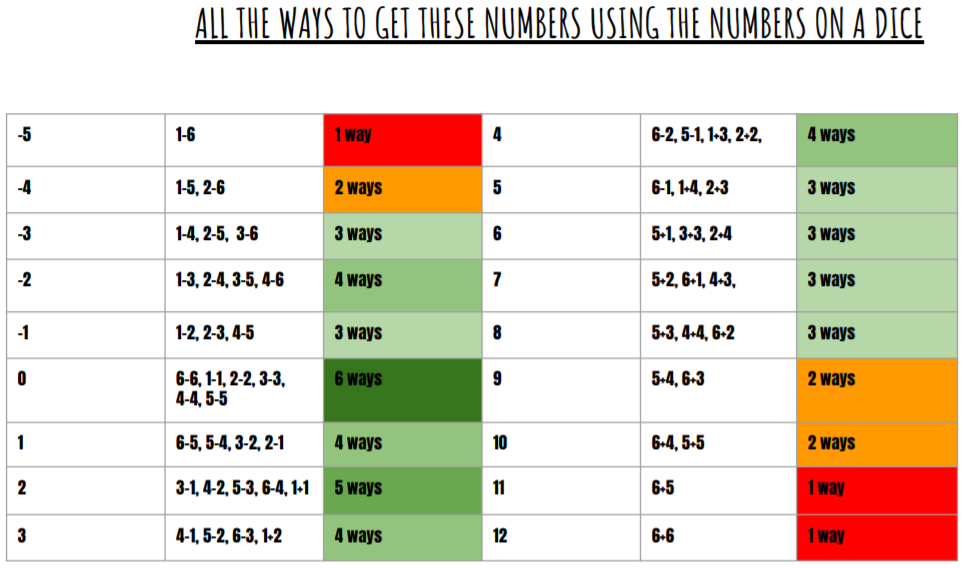 click to see full size  

click to see full size

click to see full size



Caleb from Kilvington in Australia used this idea to work out which lines connecting 3 numbers are most likely to be the winning lines:
The most likely 3 in-a-rows you can get are: 5,6,7 ; 6,7,8 ; -1,0,1 ; 0,1,2.
The most likely 3 in-a-diagonals you can get are: 1,5,9 ; -2,2,6.
The most likely 3 in-a-columns you can get are: -2,3,8 ; -3,2,7 ; -1,4,9, ; 0,5,10.
All of these methods use at least two of the numbers from -1 to 8. Also, the methods that are COMPLETELY made up of numbers from -1 to 8 give you the highest probability of winning. This is why I believe that in this game you must aim for -1 to 8.