Skip over navigation

Tug Harder!

Age 7 to 11

Challenge Level Yellow star

Primary curriculum

Tug Harder!

Tug Harder! printable sheet

You might like to try Tug of War before trying this.

This game is for two players.
You will need to draw a number line from -13 to 13 on a piece of paper, and find a counter and two 1-6 dice to use.

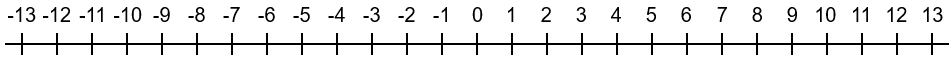
Decide who is Positive and who is Negative.
Positive moves the counter from left to right and Negative moves the counter from right to left. (Why do you think we have suggested this way round?)

Place the counter on 0.

Take it in turns to throw the two dice and add the scores then move the counter that number of places in your direction.
If the counter reaches -13, Negative has won. If the counter reaches 13, Positive has won.

Is it better to play a game where you have to reach the end exactly, or where you can go over the end? What do you think and why?

Now change the game. This time, when you throw the dice, you can decide whether to add, subtract, multiply or divide the numbers on the dice. You must reach -13 or 13 exactly to win.

Does this make a better game? What do you think? Why or why not?

How else could you change the game?

Why do this problem?

This game reinforces negative numbers and their relationship to positive numbers. The second version takes the game to a higher level as pupils will be making decisions as to which calculation to perform and why.

Possible approach

Start by dividing the class into two teams, one Positive and one Negative, to play against each other on the board. Throw two dice and call out the numbers for each team's turn, inviting a child to come up and move the counter each time. Having played a few times, ask the children whether they think it would be a better game if the counter has to reach the end exactly. Decide on some new rules to test this out and ask the children to play in pairs. It is a valuable activity in itself for them to draw out their own number line.

Bring the class together and ask which version of the game they thought was better and why. Listen out for children who back up their opinion with a clear reason. Next, introduce a new version whereby children can add, subtract, multiply or divide the dice numbers. Play in two teams using the board again to get a feel for this new game. Each time you throw the dice, ask the children what the possibilities are and discuss which would be best in terms of the move to be made and why. Then invite pairs to play on paper (they can decide whether the counter needs to reach the end of the board exactly or not).

In the plenary, ask the class which version of the game they thought was best and why. In this case, draw out responses which indicate that the choice of operation means players are more in control. You could suggest that children invent their own rules to make better games, perhaps over a longer period of time, and you could dedicate an area of your wall to their ideas.

Key questions

Is it better to play a game where you have to reach the end exactly, or where you can go over the end? Why?

Shall we add, subtract, multiply or divide the two numbers? Why?

Is it better to play a game where you can choose the operation you apply to the numbers on the dice? Why?

Can you think of some different rules of your own?

What makes your game better than the other versions?

Possible extension

You could take the mathematics in the game further still by explicitly discussing addition and subtraction using negative numbers.

Wendy Tebbatt wrote to suggest a variation of the game that she plays with her learners:

Using a number line from -20 to +20, each child has a counter on zero. Each child has a positive red dice and a negative blue dice. They take it in turns to throw both their dice together and work out how many places
they move and in which direction. For example, for red 3 and blue 5, the calculation would be 3-5=-2 so they move 2 towards -20. The first one to fall off either end is the winner. Some children can 'hop' up the positives and down the negatives whilst others may calculate before moving their counter. I often use numbers in a snake on the floor so the kids can hop up and down the number line.

Possible support

Learners could play Tug of War before they try this version of the game. You may want to have multiplication squares available so that children do not worry about the calculations as such but concentrate on the strategy.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Tug Harder!

Tug Harder!

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

Pebbles

Bracelets

Sweets in a Box