Skip over navigation
Flow charts give very precise instructions, to perform a task or calculation.
The flow chart below uses three variables of which you can choose the starting value for M.
Select several values for M and try to establish what the flow chart does.
A printable version of the flow chart is available here
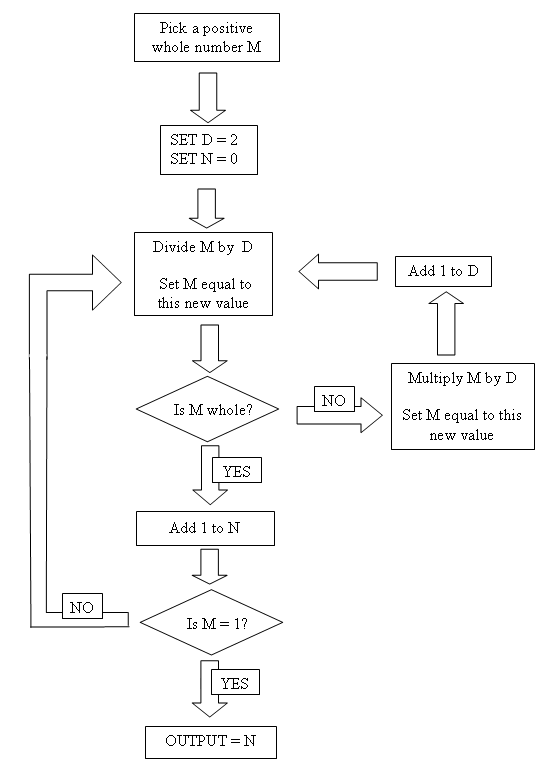
If you start with certain numbers you reach the OUTPUT fairly quickly, but if you start with other numbers you don't.
e.g. if you start with 144 you reach the OUTPUT a lot sooner than if you start with 145.
What is special about the numbers that lead to an OUTPUT quickly?
What is special about the numbers that don't?
Certain values of D divide exactly into M during the procedure?
What is special about these values of D?
What is special about the value of N that you end up with?
How can the flow chart help you determine whether M is prime?
Flow Chart
Age 11 to 14
Challenge Level 
Flow charts give very precise instructions, to perform a task or calculation.
The flow chart below uses three variables of which you can choose the starting value for M.
Select several values for M and try to establish what the flow chart does.
A printable version of the flow chart is available here
If you start with certain numbers you reach the OUTPUT fairly quickly, but if you start with other numbers you don't.
e.g. if you start with 144 you reach the OUTPUT a lot sooner than if you start with 145.
What is special about the numbers that lead to an OUTPUT quickly?
What is special about the numbers that don't?
Certain values of D divide exactly into M during the procedure?
What is special about these values of D?
What is special about the value of N that you end up with?
How can the flow chart help you determine whether M is prime?
You may also like
Simple Counting Machine
Can you set the logic gates so that the number of bulbs which are on is the same as the number of switches which are on?