Skip over navigation
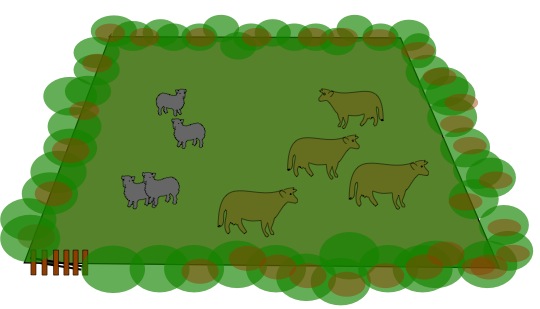
In this field we could say, because of the number of animals there, that each cow can see 4 sheep and 3 (other) cows. This could be worded as follows "Each cow can see one more sheep than cows." There are obviously 4 sheep and 4 cows in the field as you see it.
But here are some questions about different fields in which you have to find out how many sheep and cows there are in each field.
In field number 1, each cow can see twice as many sheep as cows; each sheep can see the same number of sheep as cows, so how many cows and sheep are there?
In field number 2, each cow can see three times as many sheep as cows; each sheep can see the same number of sheep as cows, so how many cows and sheep are there?
In field number 3, each cow can see twice as many sheep as cows; each sheep can see one more sheep than cows, so how many cows and sheep are there?
In field number 4, each cow can see twice as many sheep as cows; each sheep can see two more sheep than cows, so how many cows and sheep are there?
In field number 5, each cow can see three times as many sheep as cows; each sheep can see twice as many sheep as cows, so how many cows and sheep are there?
Cows and Sheep
Age 7 to 11
Challenge Level 
In this field we could say, because of the number of animals there, that each cow can see 4 sheep and 3 (other) cows. This could be worded as follows "Each cow can see one more sheep than cows." There are obviously 4 sheep and 4 cows in the field as you see it.
But here are some questions about different fields in which you have to find out how many sheep and cows there are in each field.
In field number 1, each cow can see twice as many sheep as cows; each sheep can see the same number of sheep as cows, so how many cows and sheep are there?
In field number 2, each cow can see three times as many sheep as cows; each sheep can see the same number of sheep as cows, so how many cows and sheep are there?
In field number 3, each cow can see twice as many sheep as cows; each sheep can see one more sheep than cows, so how many cows and sheep are there?
In field number 4, each cow can see twice as many sheep as cows; each sheep can see two more sheep than cows, so how many cows and sheep are there?
In field number 5, each cow can see three times as many sheep as cows; each sheep can see twice as many sheep as cows, so how many cows and sheep are there?
You may also like
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.
Sending Cards
This challenge asks you to investigate the total number of cards that would be sent if four children send one to all three others. How many would be sent if there were five children? Six?
Dice and Spinner Numbers
If you had any number of ordinary dice, what are the possible ways of making their totals 6? What would the product of the dice be each time?