Triangle Shapes

Triangle Shapes

Here are two triangles. We're going to see what shapes we can get by using many of them.

You will need to print off this sheet of triangles to cut out and use.

 

You might try putting them together like this:

Try making that or something similar.

Sometimes you can make "jewel-like" shapes:

 

See what "jewels" you can make.

 

You might make the triangles from different materials, or use an overhead projector transparency so that they are a bit transparent, then you can overlap them:

When you do that, you might try to see what shapes you've made at the overlap.

 

Maybe you could experiment further with this idea and create pictures like these:

 

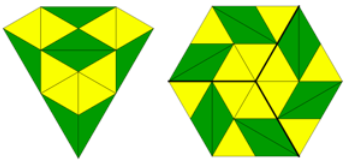
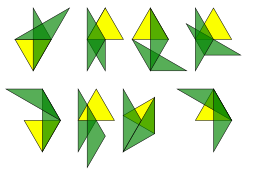
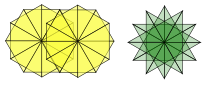
Please do send in pictures of the shapes you make, whether they include overlaps or not.
Tell us what you notice about the shapes you've made.
 

Why do this problem?

This open-ended activity is designed to allow children to demonstrate their mathematical creativity. With the freedom to use the triangles in any of the three ways, pupils will develop their own criteria to satisfy. They may choose to focus on, for example, aspects of symmetry, or on repeated pattern, or on creating particular shapes, whether in outline or in overlap...

Possible approach

To start the group off, you could make, or print off, one of each suggested "type" of arrangement. It would be a good idea to have one of them partially completed so that you can ask the children how they might continue it and why. In discussing reasons for building up an arrangement in a particular way, you will be offering opportunities for the pupils to use language associated with shape and possibly symmetry (amongst other things) and to share their ideas with each other. This will stimulate more ideas for making their own.

They could work in pairs, or individually, to make an arrangement of the triangles for themselves and as they work, move around the class, talking to them about how and why they have chosen that arrangement. Having cut out triangles available would be ideal - you could print off this sheet. You might like to ask one or two pupils to make their design for the rest of the class to talk about. These two particular triangles are chosen as they share a common measurement and you could probe this a little with the children.