Skip over navigation
Suppose we start with two types of triangles:
We will be putting them together to make 3D shapes.
Sometimes you need tabs to glue them together so you cut those out like these (here is a sheet of triangles with tabs):
Triangular Faces
Age 7 to 11
Challenge Level 
Triangular Faces
Suppose we start with two types of triangles:
and we have lots of them ready to cut out and use (you could print off this sheet).
We will be putting them together to make 3D shapes.
Sometimes you need tabs to glue them together so you cut those out like these (here is a sheet of triangles with tabs):
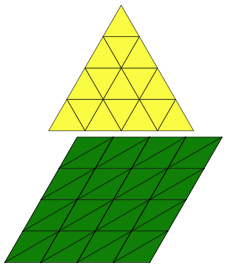
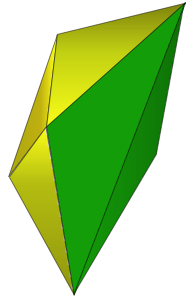
Well here is an image of 3D shape number 1 made from 6 green and 4 yellow triangles:
and here is a net that could be used to make it:
Have a go at making this or something similar. You might make it from a net or just by sticking the triangles together.
-----------------------------------------------------
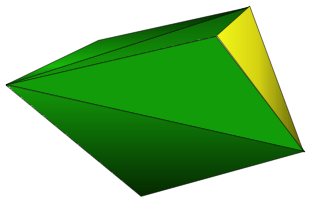
Here is an image of 3D shape number 2:
This was made from 6 yellows and 2 greens.
Can you try and make it, and work out a net for it?
-----------------------------------------------------
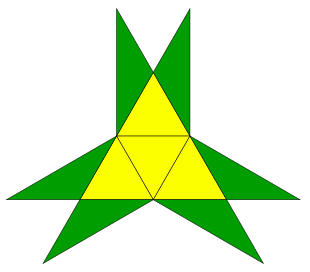
Here is the last one of mine to try, made from 4 green and 2 yellow:
See if you can make this one and discover a simple net for it.
Why do this problem?
This activity encourages children to visualise 3D shapes and will help to reinforce language associated with properties of shapes.Possible approach
You could introduce the problem by creating a simpler model of your own, made from the triangles (perhaps a tetrahedron). Show it to the class (making sure you turn it around for them to see it from different directions) and ask them what questions they would ask if you challenged them to make an identical model themselves. They might suggest:- How many faces (or how many triangles) does the shape have?
- Are all the faces (or triangles used) the same?
- How do the faces join to each other?
The children could try to make a tetrahedron and then you could look at its net together before moving on to the more complex shapes in the main problem.
As they engage with the practical element of this task, give children freedom to "change their mind" if they make a mistake, allowing them to take the triangles apart again. This act of varying and altering is an important mathematical process. As you look together at the nets they create (which could be recorded on paper), children may discover for the first time that a shape's net can be
drawn in several different ways.
Finally, you could ask the class to make some 3D shapes of their own, perhaps in pairs. Two pairs could then join together to see if they can each make the other's shape after they have had a good look.
You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?