Skip over navigation
What do you need to find a chosen number from this hundred square?
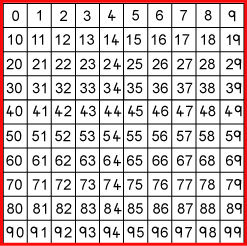
Four of the clues below are true but do nothing to help in finding the number.
Four of the clues are necessary for finding it.
Here are eight clues to use:
Can you sort out the four clues that help and the four clues that do not help in finding it?
What Do You Need?
Age 7 to 11
Challenge Level 
What Do You Need?
What do you need to find a chosen number from this hundred square?
Four of the clues below are true but do nothing to help in finding the number.
Four of the clues are necessary for finding it.
Here are eight clues to use:
- The number is greater than $9$.
- The number is not a multiple of $10$.
- The number is a multiple of $7$.
- The number is odd.
- The number is not a multiple of $11$.
- The number is less than $200$.
- Its ones digit is larger than its tens digit.
- Its tens digit is odd.
Can you sort out the four clues that help and the four clues that do not help in finding it?
Why do this problem?
This problem is an accessible context in which pupils can apply their knowledge of number properties. It is a great opportunity to get children explaining their reasoning to others.
Possible approach
Before trying this problem, it would be useful for the class to work on One of Thirty Six , perhaps in pairs. One of Thirty Six introduces the idea of using information in a particular order, which also applies to this problem.
Having discussed the solution of One of Thirty Six, present this problem to the group. (It might be useful to print out copies of it from this sheet.) Before setting the children off on this new challenge, ask whether they can already suggest some clues that are not needed. For example, the
most obvious thing might be that the "less than $200$" clue is redundant, given the grid only goes up to $99$. Suggest that pairs work on the problem, recording whatever and however they find useful. Let them know that you will be asking them to explain and justify their reasoning, as opposed to simply focusing on the answer, in the plenary.
Key questions
Which clues do you have to have to find the number?
Which clues don't tell you any more information?
Can you explain why?
Possible extension
Children could make up their own similar problem for a partner to work on. The challenge here is to include exactly four clues that are needed and exactly four that are superfluous.
Possible support
Encouraging children to shade or colour the grid somehow to reflect the information in each clue at a time might be helpful. Having the clues written on individual pieces of paper is a good way for each one to be read individually, and they can be grouped easily according to which are useful and which are not.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Roll These Dice
Roll two red dice and a green dice. Add the two numbers on the red dice and take away the number on the green. What are all the different possible answers?
