One of Thirty-six

Age 5 to 7

Challenge Level Yellow star

We had so many well-explained solutions to this problem - thank you all very much.

Adeline told us:

According to the first and second statements the only possibilities are 3, 9, 15, 21, 27 and 33.
If the third statement then says that it is smaller than 28 (7x4) then the remaining numbers off the list are 3, 9, 15, 21 and 27.
It then says that the tens digit has to be even so then the numbers 3 and 9 are immediately scraped off (because they don't have a tens digit!) leaving 15, 21 and 27. 15 has the tens digit 1 which is not even leaving the only two possibilities 21 and 27.
The last statement then says it is the bigger of the two and that is 27. So the number is 27.

Kaitlyn from Mason Middle School made a table to help her:

The answer is 27. I know this because I used the process of elimination with the given hints. The way I did this was:

Hint	Possible numbers
The number is odd	1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35
The number is a multiple of three	3,9,15,21,27,33
It is smaller than 7x4 (=28)	3,9,15,21,27
The tens digit is even	21,27
It is the greater of the two possibilities	27 because that is greater than 21

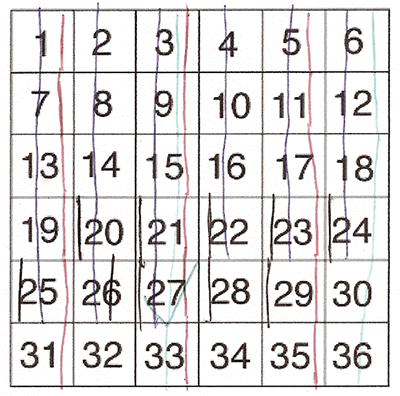
Dylan from Oakland Township Elementary used a similar method, but he explains how he used the number grid itself to write on:

The clues 1 and 2 were the easiest to figure out. For clue 1, I circled all the odd numbers. Odd numbers are the numbers that multiples of two never touch.

For clue 2, I took all the multiples of three and circled them and crossed off the other odd numbers. Multiples of three are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, and 36. It is like counting by threes.

When clue number 3 came on, it stumped me for about 10 seconds. Then I found a different way of doing it. I decided to read clue 4 and come back to clue 3. I crossed off all the numbers with an odd number or no number for their tens.

I went to 7x4 and figured out that it is 28. I crossed off all the numbers bigger than 28.

Finally, it was the bigger number between 27 and 21, which 27 was bigger than 21. And that is how I got my solution of 27.

Thank you, Dylan. Crossing out or circling the numbers as you go along can help you keep track of what you're doing. Daniel from Engelfield Green Infants School did this too. Here is what Daniel wrote:

I printed off the square with the numbers.

I put a red line through all the squares with odd numbers.

I put a green line through all the squares with numbers that were multiples of three.

I put a blue line through all the squares with numbers that were smaller than 28 (7 x 4).

I put a black line through all the squares with numbers where the tens digit was even.

I found that there were two squares with all the colours: 21 and 27. The solution is 27 because it is bigger than 21 by 6.

Here is a picture of Daniel's work:

Thank you again for all your contributions to this problem. I'm afraid there are too many to mention you all!

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

One of Thirty-six

You may also like

Number Round Up

Number Detective

Grouping Goodies