Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Unusual Long Division - Square Roots Before Calculators
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem takes more able students into the realm of 'non-calculator' methods that lie beyond the arithmetic they became familiar with when they were much younger. It usefully draws attention to the need for validation in any algorithm whether carried out electronically or 'by hand'.Possible approach
- Spend a little time looking at the validity of the standard method for 'Long Division'. Discuss the historical need for efficient algorithms before electronic calculators, when computation was manual, and point out that calculators and computers aren't 'magic' and there still has to be a valid algorithm.
- Find some square roots of two-digit numbers to 2dp by trial and improvement.
- Spend time understanding what this new method involves (maybe use the audio link on the Problem page ,while keeping the working still on view), practise and then organise a time trial.
- Alternate between this method's algorithm and trial & improvement, for the square roots of 30, 50, 60, 70, 80, and 90, all to two decimal places. Record the calculation time for each one and compare methods.
Key questions
-
How do we find the square root of 40 on a calculator that only does simple '4 rules' arithmetic?
-
What exactly is the method here?
Possible extension
Explain that a mathematician will always want to justify or validate a procedure and leave that challenge with the group.Possible support
For less able students raising awareness that methods of calculation need justifying can lead to a stronger and more satisfying grasp of arithmetic procedures like 'long multiplication' (traditional and alternative) and 'long division'.You may also like
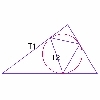
Triangle Incircle Iteration
Keep constructing triangles in the incircle of the previous triangle. What happens?
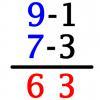
Vedic Sutra - All from 9 and Last from 10
Vedic Sutra is one of many ancient Indian sutras which involves a cross subtraction method. Can you give a good explanation of WHY it works?
Tournament Scheduling
Scheduling games is a little more challenging than one might desire. Here are some tournament formats that sport schedulers use.

