Weights
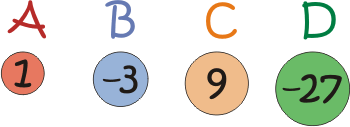
Imagine you have two of each of the 'weights' above.
Different combinations of the weights available allow you to make different totals.
For example:
$B + 2C = 15$
$A + 2B + C = 4$
$2A + B + 2C + D = -10$
The largest total you can make is $20$ (check you agree).
The smallest total you can make is $-60$ (again, check you agree).
Can you make all the numbers in between?
Is there always a unique way of producing a total, or can different combinations produce the same total?
Extension:
If you are allowed just three different weights this time ($E$, $F$ and $G$), and at least one must be a negative weight, and you are now allowed to have up to three of each, you could choose:
$F = -4$
$G = 5$
You could make $7$ and $-10$:
$2E + 3F =$ $-10$
Choose your three weights and test out which totals you can make.
Which set of three weights ($E$, $F$ and $G$) allows you to make the largest range of totals with no gaps in between?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Related Collections
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Pair Sums
Five numbers added together in pairs produce: 0, 2, 4, 4, 6, 8, 9, 11, 13, 15 What are the five numbers?
Negative Dice
If the odd numbers on two dice are made negative, which of the totals cannot be achieved?