Skip over navigation
Steve looked at making each type of gates from NANDs
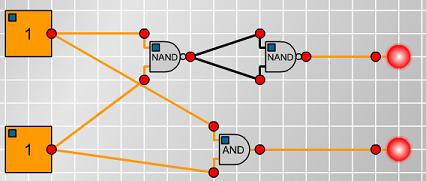
I used the circuit maker to investigate. I first made a circuit which seemed symmetrical in the NAND gates. This matched the AND gate, as shown here:
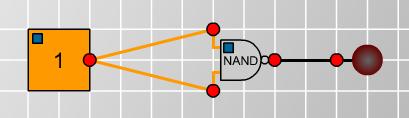
I then realised that directing the same current into both inputs of the NAND gate would be like a NOT
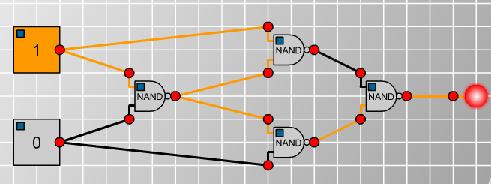
Since I can make a NOT, I now only need to find the OR and XOR circuits. Both would need to be symmetrical in the two input gates. A first trial gave me this circuit. Playing with the switches showed this to be XOR
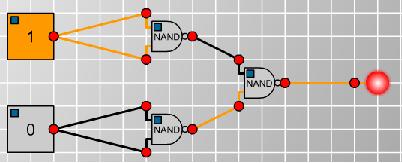
The final gate was an OR. I didn't experiment with this, because I realised that $A \textrm{ OR } B$ is like [NOT($A$)] NAND [NOT($B$)], so could use the NOT gate construction from before.
This was very satisfying and nice and clean.
Steve then thought about the concept of the universal gate for the other inputs types.
As for the second part, it is clear that OR is always on if a current is passed into it: therefore there will be no way of OR gates making a NOT gate; OR cannot, therefore, be universal.
NOT gates can't be universal, because they only take one input.
For a circuit with two inputs constructed entirely of AND gates if the inputs are both off then the output must also be off. Thus, we cannot construct NAND with just and gates. Therefore, AND is not universal. The same is true for a circuit constructed entirely of XOR gates. This is interesting, as I realise that a universal gate must be able to produce an output of 1 from 0 inputs.
Thus, the only possible remaining candidate for a universal gates is XNOR. I didn't try this any further, but this could be experimented with on a circuit board.
Doug looked at the question of whether other sorts of logic gates were universal, exploring the possibilities for two- and three-input logic gates
Assuming two-input gates, if you write out a truth table for two inputs $A$ and $B$, for XOR, XNOR, OR and AND, each gives a certain output $C$. If you use the same function to combine $C$ with one of the original inputs, you get one of the original inputs, in all four of these cases. Therefore you could go on forever and never get a NAND from any of these, therefore they are not universal. Clearly NOT is not universal since it only takes a single input.
NOR is universal. There is technique for analysing logic expressions called a "Karnaugh map" (http://en.wikipedia.org/wiki/Karnaugh_map), and if you "map the zeros", you can express any logic table with NORS.
However, it does make sense to have three-or-more-input gates for all of these logical gates except NOT. And for example a three-input XOR can be converted to a two-input XOR by setting one of the inputs to logical 0, so this hugely increases the possibilities. I wrangled with XOR for about 45 minutes and found that (let $\%$ signify XOR, and $\cdot$ signify AND)
$$A \cdot B \cdot C = (\ A\ \% \ B \ \% \ C \ ) \ \% \ A \ \% \ (\ B \ \% \ C \ )$$
(the order of the last 3 can be changed as you'd expect, but the brackets are required).
If you then XOR with logical 1 (and the rest 0 for more than two-input gates), you have a NOT gate, so I can NOT the AND to get a three-way NAND gate. And if we set one of the inputs of the three-way NAND gate to logical 1, we have a two-input NAND gate.
Having realised this, I went back and checked a two-input XOR including the possibility of using it as a NOT, but it is still not possible to get a NAND from it. Including the not function, and two general inputs $A$ and $B$, you can get every possible output that includes two 1s and two 0s, i.e. $^4C_2 = 6$ possible truth tables. NOTing, or XORing any such state with any other such state always results in another such state, so there are no other truth tables (of the $2^4 = 16$ that can exist) that can be achieved with XOR gates.
So a three-input XOR gate is universal, but a two-input XOR gate is not.
The three-input XOR function can be expressed as
$$\overline{\overline{\overline{C} \cdot \overline{A}\cdot B}\cdot\overline{\overline{C}\cdot A \cdot \overline{B}}\cdot \overline{C \cdot \overline{A}\cdot \overline{B}}}$$
which can be made with NANDs (and easily found using a "Karnaugh map"), so you can satisfy yourself that a three-input XOR gate can be built from the bottom up with components, just as a NAND gate is.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Not Another NAND!
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Steve looked at making each type of gates from NANDs
I used the circuit maker to investigate. I first made a circuit which seemed symmetrical in the NAND gates. This matched the AND gate, as shown here:

I then realised that directing the same current into both inputs of the NAND gate would be like a NOT

Since I can make a NOT, I now only need to find the OR and XOR circuits. Both would need to be symmetrical in the two input gates. A first trial gave me this circuit. Playing with the switches showed this to be XOR

The final gate was an OR. I didn't experiment with this, because I realised that $A \textrm{ OR } B$ is like [NOT($A$)] NAND [NOT($B$)], so could use the NOT gate construction from before.

This was very satisfying and nice and clean.
Steve then thought about the concept of the universal gate for the other inputs types.
As for the second part, it is clear that OR is always on if a current is passed into it: therefore there will be no way of OR gates making a NOT gate; OR cannot, therefore, be universal.
NOT gates can't be universal, because they only take one input.
For a circuit with two inputs constructed entirely of AND gates if the inputs are both off then the output must also be off. Thus, we cannot construct NAND with just and gates. Therefore, AND is not universal. The same is true for a circuit constructed entirely of XOR gates. This is interesting, as I realise that a universal gate must be able to produce an output of 1 from 0 inputs.
Thus, the only possible remaining candidate for a universal gates is XNOR. I didn't try this any further, but this could be experimented with on a circuit board.
Doug looked at the question of whether other sorts of logic gates were universal, exploring the possibilities for two- and three-input logic gates
Assuming two-input gates, if you write out a truth table for two inputs $A$ and $B$, for XOR, XNOR, OR and AND, each gives a certain output $C$. If you use the same function to combine $C$ with one of the original inputs, you get one of the original inputs, in all four of these cases. Therefore you could go on forever and never get a NAND from any of these, therefore they are not universal. Clearly NOT is not universal since it only takes a single input.
NOR is universal. There is technique for analysing logic expressions called a "Karnaugh map" (http://en.wikipedia.org/wiki/Karnaugh_map), and if you "map the zeros", you can express any logic table with NORS.
However, it does make sense to have three-or-more-input gates for all of these logical gates except NOT. And for example a three-input XOR can be converted to a two-input XOR by setting one of the inputs to logical 0, so this hugely increases the possibilities. I wrangled with XOR for about 45 minutes and found that (let $\%$ signify XOR, and $\cdot$ signify AND)
$$A \cdot B \cdot C = (\ A\ \% \ B \ \% \ C \ ) \ \% \ A \ \% \ (\ B \ \% \ C \ )$$
(the order of the last 3 can be changed as you'd expect, but the brackets are required).
If you then XOR with logical 1 (and the rest 0 for more than two-input gates), you have a NOT gate, so I can NOT the AND to get a three-way NAND gate. And if we set one of the inputs of the three-way NAND gate to logical 1, we have a two-input NAND gate.
Having realised this, I went back and checked a two-input XOR including the possibility of using it as a NOT, but it is still not possible to get a NAND from it. Including the not function, and two general inputs $A$ and $B$, you can get every possible output that includes two 1s and two 0s, i.e. $^4C_2 = 6$ possible truth tables. NOTing, or XORing any such state with any other such state always results in another such state, so there are no other truth tables (of the $2^4 = 16$ that can exist) that can be achieved with XOR gates.
So a three-input XOR gate is universal, but a two-input XOR gate is not.
The three-input XOR function can be expressed as
$$\overline{\overline{\overline{C} \cdot \overline{A}\cdot B}\cdot\overline{\overline{C}\cdot A \cdot \overline{B}}\cdot \overline{C \cdot \overline{A}\cdot \overline{B}}}$$
which can be made with NANDs (and easily found using a "Karnaugh map"), so you can satisfy yourself that a three-input XOR gate can be built from the bottom up with components, just as a NAND gate is.
You may also like
Adding Machine
Can you set the logic gates so that this machine can decide how many bulbs have been switched on?

