Skip over navigation
By Henry Kwok
Here
is a Word document with the two Sudoko grids that you can download
for printing.
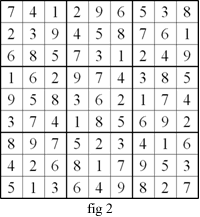
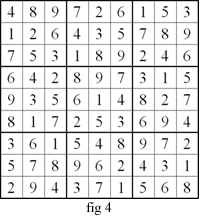The four puzzles (fig 1 to fig 4) are equivalent to one another.
Equivalent puzzles can also be created from fig 1 and fig 2 by
renaming the elements in the respective grids. Instead of calling
fig 1 and fig 4 by the clumsy name of 'twin element-renaming
chute-swapping sudoku', we can simply call them 'twin equivalent
sudoku'.
Twin Equivalent Sudoku
Age 16 to 18
Challenge Level 
By Henry Kwok
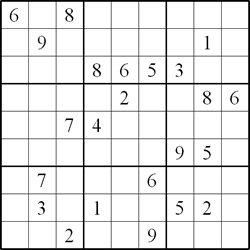
| Twin A | Twin B |
 |
 |
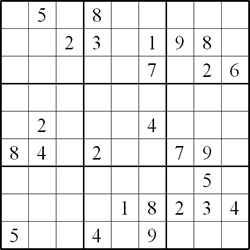Rules of Twin Equivalent Sudoku
This Sudoku consists of a pair of linked standard Sudoku
puzzles each with some starting digits. As usual, the object of
this Sudoku is to fill in the whole of each 9x9 grid with digits 1
through 9 so that each row, each column and each block contain all
the digits 1 through 9.
Twin B is related to twin A in the following ways:
1. Given that twin A is the original puzzle, we can create an
equivalent puzzle from twin A by swapping a horizontal/vertical
chute or band of 3 blocks with another horizontal/vertical chute or
band of 3 blocks.
For example, an equivalent puzzle (fig 2) is created from fig
1 by swapping the left vertical chute of 3 blocks with the middle
vertical chute of 3 blocks.
Similarly an equivalent puzzle (fig
3) can be created from fig 1 by swapping the top horizontal chute
of 3 blocks with the middle horizontal chute of 3 blocks.
2. After swapping the chutes, we can create a third equivalent
puzzle (twin B) by renaming all the elements of second equivalent
puzzle.
For example, we create an equivalent puzzle (fig 4) by
renaming the elements of fig 3 in the following way:
fig 3 $\rightarrow $ fig 4
$1 \rightarrow7 $
$ 2 \rightarrow 6 $
$ 3\rightarrow 1 $
$4 \rightarrow 9 $
$ 5 \rightarrow 3 $
$6 \rightarrow 2 $
$7 \rightarrow 8 $
$8 \rightarrow 5 $
$9 \rightarrow 4$
You may also like
Instant Insanity
Given the nets of 4 cubes with the faces coloured in 4 colours, build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.