Simultaneous Equations Sudoku

 

 

 

 

 

 

 

 

 

Since the difference between $c+g+k$ and $k+g+m+c$ is $m,$ $m$ is $23-17$ which is $6.$
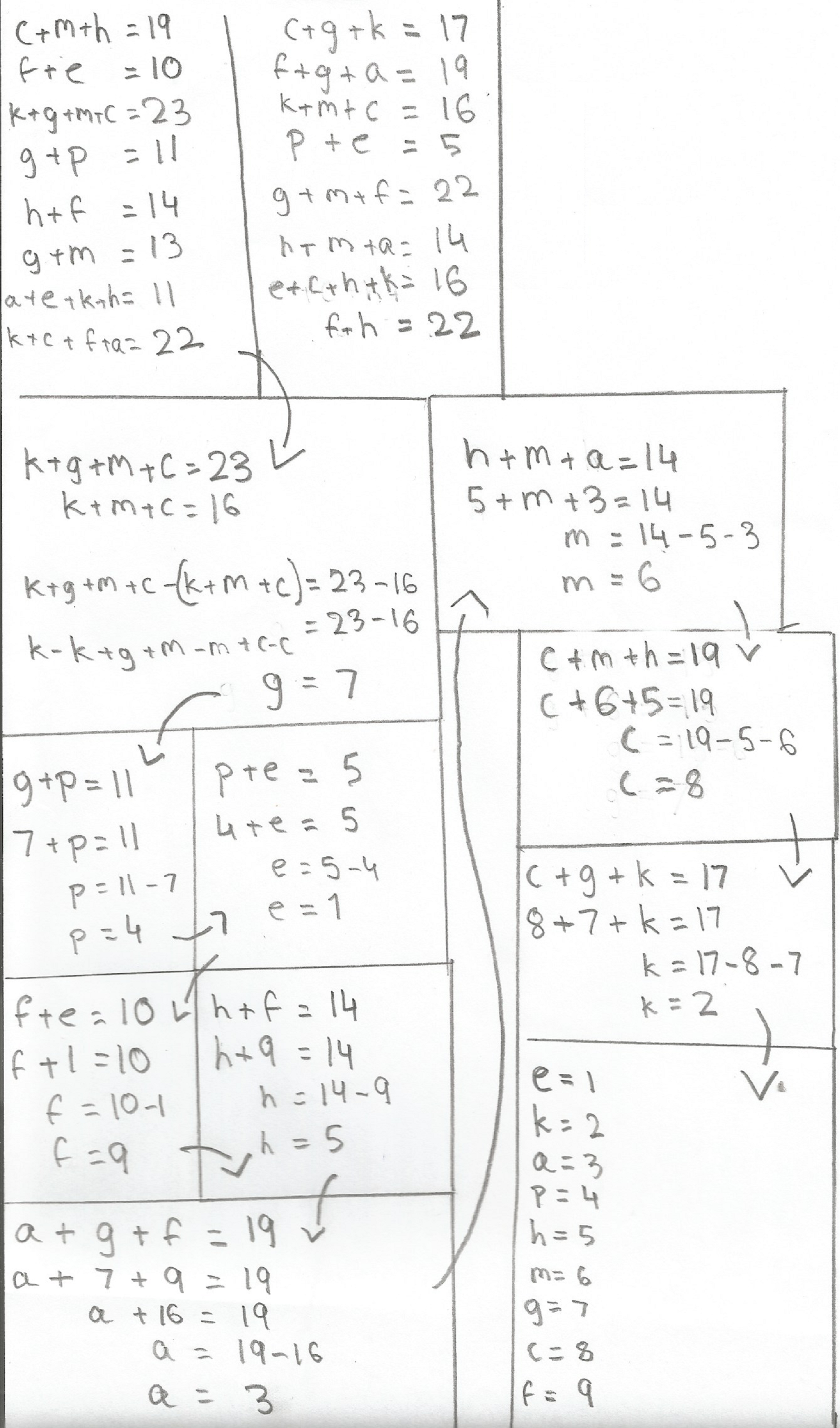
In the third row up, $g$ must be $7$ as $13-6=7.$
In the fifth row, $p$ must be $4$ since $11-7=4.$
In the sixth column, $f$ is $9$ since $22-13=9.$
In the second row, $e$ must be $1$ because $10-9=1.$
In the sixth row, $h$ is $5$ since $14-9=5.$
In the first row, $c$ is $8$ because $19-11=8.$
In the first column, $k$ must be $2$ as $17-15=2.$
By process of elimination, $a$ must be $3,$ but with this information you could easily work that out.

 

1st Step: Find the values of the variables in the sudoku.
Since $g + m = 13$ and $g + m + f = 22,$ therefore $13 + f = 22$ and $f = 9.$
Since $f = 9$ and $f + h = 14,$ therefore $h = 5.$
Since $f = 9$ and $f + e = 10,$ therefore $e = 1.$
Since $e = 1$ and $p + e = 5,$ therefore $p = 4.$
Since $p = 4$ and $g + p = 11,$ therefore $g = 7.$
Since $f = 9, g = 7$ and $f + g + a = 19,$ therefore $a = 3.$
Since $g = 7$ and $g + m = 13,$ therefore $m = 6.$
Since $m = 6, h = 5$ and $c + m + h = 19,$ therefore $c = 8.$
Since $c = 8, g = 7$ and $c + g + k = 17,$ therefore $k = 2.$

2nd Step: Solve the sudoku.
After finding out what the variables represent, draw up a grid and write the numbers (that you have found) in the place of the variables. This should make it easier to solve the sudoku. Now there's the usual sudoku that you can solve. I solved mine by filling out all the 6's first, then gradually worked down the possibilities of where the numbers can go.