Skip over navigation
Circuit Maker
Age 11 to 18
Challenge Level 
Why do this problem?
This problem gives the simplest introduction into logic gates and circuits. Through experimentation with switches, students will begin to see the structure of logic gates emerge without the need for any detailed formalism. They will then see that logic gate circuits can be constructed using a more complicated approach.Possible approach
Put the problem on to the board. Encourage students to read the problem and decide what the circuit board means. Encourage experimentation with combinations of off /off. At each stage, encourage students to describe what they can see. How can this sensibly be recorded?
Once students feel that they understand how a gate works they should write a sentence describing the action of the gate. Do others agree that this is a clear definition? How might is be improved? Could we use it in the definition of the behaviour of the other gates?
You might like to discuss with the class how the words 'and' 'or' and 'not' are used in real life. How does this relate to logic-speak? Students might enjoy inventing logic-speak sentences such as:
'I really like eating ice cream XOR chicken curry' (meaning I like ice cream and curry, but not at the same time)
'I like tea XNOR milk' (meaning I only like tea with milk)
Key questions
- Describe what you see.
- What are we supposed to change? What are we supposed to leave fixed?
- How might we record our findings?
- What happens if the switches in the two pairs of circuits are set to the same values?
Once students feel that they have described the gates clearly using English, usethis follow up
- How could you represent the behaviour of the gate symbolically?
Possible extension
Once the concept of the gate is understood there are several follow up questions, such as Simple Counting Machine .
Possible support
You might suggest focussing on the AND, OR and NOT gates to begin withRelated Collections
You may also like
Just Rolling Round
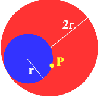
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
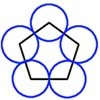
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Cushion Ball
The shortest path between any two points on a snooker table is the straight line between them but what if the ball must bounce off one wall, or 2 walls, or 3 walls?