Skip over navigation
Article by Leo Rogers
A proof of a mathematical statement is a logical argument that shows the statement is true according to certain accepted standards.
The idea of proving a statement is true is said to have begun in about the 5th century BCE in Greece where philosophers developed a way of convincing each other of the truth of particular mathematical statements. They had to agree definitions of certain basic ideas (e.g. point, line, surface), and axioms [see note 1 below ] which were statements about the starting points (e.g. that it is possible to draw a circle of any radius). Over time these ideas and many others were developed in geometrical form, and finally collected and organised in thirteen Books by Euclid (325-263 BCE) in what was called his "Elements of Mathematics".
Ideally, the proof of a statement in any particular branch of mathematics uses the rules, definitions, axioms and theorems of that branch of mathematics, together with the rules of logic. Even though arithmetic, algebra and geometry each have different rules and procedures, we use the same kind of logic for each of them.
In the 5th and 6th centuries BCE, the Pythagoreans [see note 7 below ] were interested in finding a common measure for the side of a square and its diagonal and discovered that these two lengths were incommensurable [see note 8 below ] by using a geometrical construction. In geometrical terms, this can be demonstrated by the successive subtraction of the smaller length from the larger:
In order to overcome some of the difficulties experienced by the
Pythagoreans, Euclid ( in Book X of his Elements) showed how to
manage the mathematics of incommensurables like $\sqrt 2, (3 +
\sqrt 5)$ , etc, [See note 10
below ] purely by geometrical constructions.
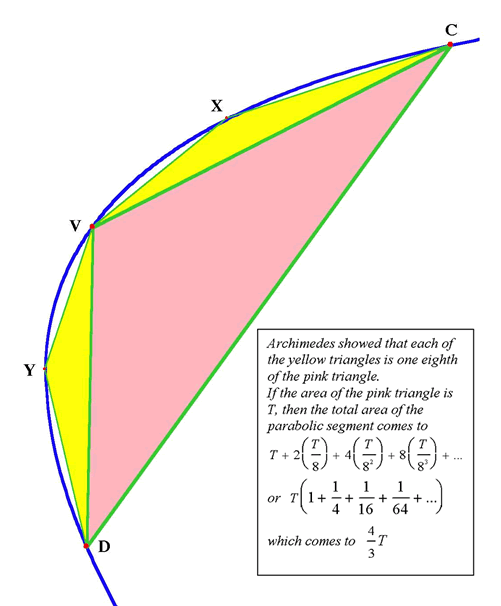
In his first proof of the area of a parabolic segment, Archimedes
used his discovery of the properties of the lever to balance the
weight of a segment of a parabola against the weight of a triangle.
In his second proof he used the method of exhaustion to show that
the area of the segment was $\frac{4}{3}$ that of the triangle.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Age 14 to 18
Published 2008
Proof: A Brief Historical Survey
A proof of a mathematical statement is a logical argument that shows the statement is true according to certain accepted standards.
The idea of proving a statement is true is said to have begun in about the 5th century BCE in Greece where philosophers developed a way of convincing each other of the truth of particular mathematical statements. They had to agree definitions of certain basic ideas (e.g. point, line, surface), and axioms [see note 1 below ] which were statements about the starting points (e.g. that it is possible to draw a circle of any radius). Over time these ideas and many others were developed in geometrical form, and finally collected and organised in thirteen Books by Euclid (325-263 BCE) in what was called his "Elements of Mathematics".
Ideally, the proof of a statement in any particular branch of mathematics uses the rules, definitions, axioms and theorems of that branch of mathematics, together with the rules of logic. Even though arithmetic, algebra and geometry each have different rules and procedures, we use the same kind of logic for each of them.
Direct and Indirect Proof.
Direct Proof
Direct Proof is possible if we have agreed axioms and
definitions to start from and an agreed method (a logical argument)
that enables us to proceed logically step by step from what we know
to what we do not know, but think is true.For example, propositions
5 and 6 in Euclid Book I are about the equality of the base angles
of an isosceles triangle [see
note 2 below ]. This is "obviously" true, but still has to
be proved from first principles.
For some more difficult problems mathematicians developed a
method of "working backwards". This works by assuming that the
desired result is true, and showing that the consequences of that
assumption are consistent with known facts and the basic
principles. The final proof still had to be written out in the
correct order.
Constructive proof is another form of direct proof. This is
where an object has to be directly constructed from the basic
elements of the system. There are many constructive proofs in
Euclid Book I. Proposition 1 for example, shows how to construct an
equilateral triangle [see note 3
below ].
However, it is not always possible to prove something by
keeping to the strict rules of direct proof, and so mathematicians
devised forms of indirect proof to achieve results.
Indirect Proof
Indirect proof means that we try to find a way of obtaining a
result in some "round about" way. One way is by supposing that if
the result we are looking for is not true, then the starting point
cannot be true. [see note 4
below ]
Reductio
ad Absurdum or Reduction to the Absurd [see note 5 below ] is another method
of indirect proof where we try to show the opposite of the
proposition to be true, but as soon as we come to a situation in
the argument that we know is impossible, then we can say that the
original proposition was true.
The
proof that the square root of two is not rational
[see note 6 below ] is a
classic problem where an Indirect Proof is used. A proof originally
attributed to Aristotle (384-322 BCE), uses basic ideas of
arithmetic. This proposes that the diagonal of a square can be
represented by a rational fraction, and produces an argument that
constructs a number that is both even and odd (which is not
possible of course).
In the 5th and 6th centuries BCE, the Pythagoreans [see note 7 below ] were interested in finding a common measure for the side of a square and its diagonal and discovered that these two lengths were incommensurable [see note 8 below ] by using a geometrical construction. In geometrical terms, this can be demonstrated by the successive subtraction of the smaller length from the larger:
In the red square in Figure I, BD =
AB (=AC) and if BC (the diagonal) and AC (the side) have a common
measure it must also be a common measure for CD = BC-BD.
Now AB' = B'D = DC
And B'C = AC - AB'. So B'C must
also have the same common measure.
So, in the green square, the
diagonal B'C and the side DC have the same common measure. By the
same argument as for the red square, DC' minus DD' leaves D'C'
(which again has the same common measure). This means that no
matter what the size of the square, the common measure will always
be the same. [See note 9
below ]
This is an indirect proof, because it shows that the process
goes on forever producing a lower limit which is zero -
contradicting the idea that a common measure can be found.
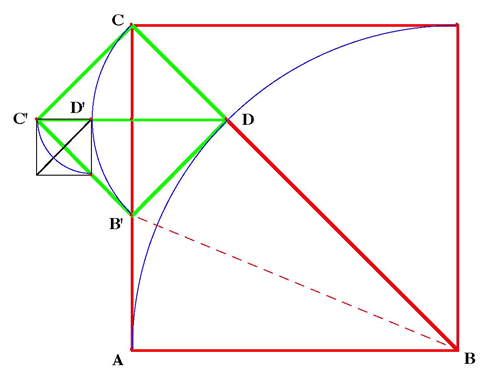 |
|
Diagram I
|
Keeping to the rules?
However, even in Euclid's Book I, the first proposition about
congruent triangles [See note 11
below ], there were unsubstantiated assumptions. Euclid used
the idea of "superposing" one triangle on another by a kind of
transformation, but there are no postulates or definitions about
what is meant by this action. In other words, even Euclid used an
idea that was not fully justified.
It is now recognised that Archimedes (287-212 BCE) developed
his own methods for calculating difficult results about areas and
volumes enclosed by curves and surfaces, and then rewrote them in
terms of the standard geometrical procedures of the time
[See note 12 below ]. In a
letter to a friend he said,
"I set myself
the task of communicating to you a certain geometrical theorem
which had not been investigated before but has now been
investigated by me, and which I first discovered by means of
mechanics and then exhibited by means of geometry."

So, the ideal proof methods set up
by the earliest European mathematicians were not always adhered to,
and later we will see that other mathematicians were still breaking
the rules in order to achieve new results.
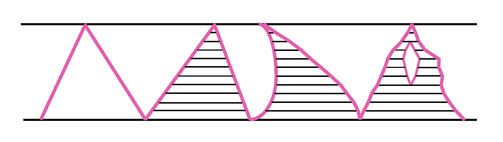
In the early ideas of the calculus, Cavalieri (1598-1647) and
others adapted Archimedes' method of exhaustion to develop the
method of "indivisibles". These were conceived of as infinitely
small elements of lines, surfaces or volumes. Arguing by analogy, a
line was made up of points, a surface was made from lines, as in
the weave of cloth, and a volume thought of as a pile of very thin
sheets of paper. In this way, areas and volumes of new objects
could be compared with areas and volumes of known objects by a
process of transformation.

For example, the area of a triangle was
thought of as a very large number of very thin parallel lines.
These were called 'Line Infinitesimals'. Areas of triangles on the
same base and between the same parallels are equal. If each line
remains the same total length, then the areas of the irregular
shapes are the same as the area of the triangle s.
Throughout the 17th century, "proof by
demonstration" was common.
The general idea was, "If I show
you enough examples of how the algorithm works, then you will be
convinced'. Mathematicians demonstrated how they achieved their results in
the early calculus by showing diagrams of curves, and sufficient
examples of the procedures to convince their audience. In most
cases the truth of the result was established by it's practical
application, or that it achieved the same results as already known
by a geometrical method. These experiments and demonstrations aided
the discovery of interesting and important results, but did not
conform to the strict standards of proof because they were based on
unjustified assumptions about the very small quantities eventually
"disappearing".
Many mathematicians were uncomfortable with this situation,
but a logical basis for the calculus methods did not appear until
the middle of the 19th century.
 |
This is part
of the first English Edition of Newton's method for discovering the
areas under curves using his method of infinite series published in
1745.
This is the
general rule for what we now call 'integration' in the
calculus.
Newton
gives examples to demonstrate how it works with different algebraic
expressions. .
|
When mathematicians like La Hire (1640-1718) and Chasles
(1793-1880) began to develop projective geometry, they used a
method called "projection and section" to show that many Euclidean
proofs were also valid in the new geometry. For example, it was
well known that the ellipse could be obtained by taking a section
through a cone, so why not think of the ellipse as a transformation
of a circle and look for the properties which remain the same?
[See note 13 below ]
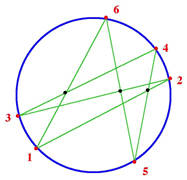 |
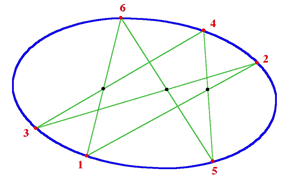 |
For example,
making an oblique cut on a circular cone produces an ellipse. By
the method of 'Projection and Section' we can imagine the ellipse
as the 'shadow' of the circle on a plane. Brianchon's (1783-1864)
theorem states that if six vertices of a hexagon on a circle are
joined as in the diagram, the intersections of the chords joining
the points as shown lie in a straight line. The same result is also
true for the ellipse or any other conic section. This is related to
Pascal's theorem where the three points of intersection of the
opposite sides of a hexagon lie in a straight line.
Imre Lakatos, in his Proofs
and Refutations tells the story of the way the proof of the
Descartes-Euler conjecture (F + V = E + 2) about counting the
Faces, Vertices and Edges of polyhedra [see note 14 below ] was challenged by
scientists working in the new field of crystallography, and how the
original definition of a polyhedron had to be changed [see note 15 below ]. For example, it
is possible to grow isomorphic [see note 16 below] crystals, one
'inside' another and there is a good argument to suggest that the
conjecture might not be valid in this case. There are many examples
where counterexamples of mathematical propositions have come from
the physical world and mathematicians have had to re-think their
theories.
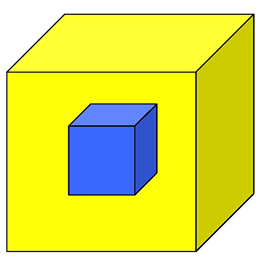 |
The blue cube
and the yellow cube are isomorphic.
Can this be
one polyhedron or two?
So F + V = E +
4?
What about a
tetrahedron inside another tetrahedron?
|
In recent times, computers have been used to investigate
solutions of difficult mathematical problems and one was used to
tackle the proof of the famous Four Colour Theorem using a program
to enumerate all possible maps [see note 17 below ]. The big question
was since all proofs up to this time had been proved by people, was
the fact that it had been completed by a computer a valid proof or
not, and how could anyone be sure the computer had covered all the
possible cases? This kind of counting procedure is called
proof by
enumeration or proof by exhaustion
.
Proof by experiment or showing examples
has always been a problem, as we have seen with the polyhedra and
the maps, since we never know whether we have all the possibilities
or when somebody will discover a counterexample. We need clear
definitions and logical argument based on agreed facts to provide a
sound proof.
Today, mathematicians have many ways of tackling proofs by
using one system to help them find results in another. For example,
Pythagoras' Theorem can be regarded as an arithmetic relation, an
algebraic generalisation, a formula in trigonometry, or as
geometric property. Each of these approaches gives different
insights into the wide range and application of the general
idea.
For this to work, it is
important to be sure that the fundamental properties remain
invariant as we transform the problem from one system to
another.
Wise Men from the East
Recently, important research in ancient Hindu and Chinese
mathematics has uncovered some very different attitudes to
"proving" results. Besides making their own original contributions,
mathematicians wrote Commentaries on the works of earlier writers
to elaborate ideas, to find other ways of achieving results, and of
making new and useful applications. It is now clear that other
cultures have produced ways of finding "truths" and generalisations
quite different from Aristotle's logic.
Indian
Mathematics
Many Indian writers who produced original mathematics, also
took great pains to write commentaries on their own works and on
works of earlier scholars. By the time of Bhaskaracharya
(1114-1185) [see note 18
below ], Indian mathematicians had achieved an understanding
of number systems and solution of equations which was well ahead of
the Europeans. It is in their commentaries that we find detailed
proofs and demonstrations of their results and discussion of
appropriate methods. Until recently, much of this was obscured by
superficial interpretation and misunderstandings of the cultural
context [see note 19 below
].
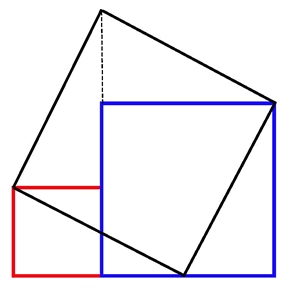 |
An ancient
Indian text, the 'Sulbasutra' (meaning 'Rope-Measuring') shows how
to use two different size squares to find the area of a square
which is the sum of the two areas.
By
discussing this diagram, students were able to justify and extend
this method, thus discovering many geometrical properties much
earlier than the Greek mathematicians .
|
Chinese
Mathematics
The most important classic of Chinese mathematics is
The Nine Chapters on the
Mathematical Art which was written some time in the 1st
century CE. Liu Hui (265-316 CE) wrote an important commentary on
this work, and recent research shows us that there are other
methods of investigating mathematical ideas other than the commonly
accepted proof methods of Euclid. During this period in China,
mathematics proceeded as a discussion between master and student
who together focussed on the diagram; its appearances and
possibilities. This shows that deduction from first principles is
not the only model for the discovery and checking of mathematical
results. This is a model of mathematical reasoning quite different
from that of Euclid, but just as important and fundamental with the
aim of generalisation rather than abstraction, and of deeper
understanding rather than logical proof.
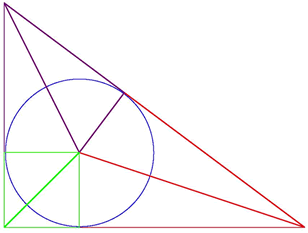 |
This
right-angled triangle comes from Lui Hui's commentary on the 'Nine
Chapters'.
By using some
simple geometry students were able to find the area of the triangle
and a number of other relations between the lines and the other
areas in the diagram. This was done quite independently from the
Greek geometers.
|
For pedagogical notes
Use the notes tab at the top of
this article or
click here .
Notes
- The Greek word 'axiom' means an agreed starting point. The word 'postulate' is also used to describe 'what is possible', or what basic ideas can be used.
- Proposition 5 used to be called the 'Pons Asinorum' (the Bridge of Asses) because it was once regarded as a test of understanding for the rest of the Elements.
- This proof has been criticised because Euclid has no axiom which states that there is a point of intersection when two lines cross.
- This is often called the contrapositive argument. i.e. If p implies q, then 'not q' implies 'not p'.
- Some mathematicians choose to call 'reductio ad absurdum' orproof by contradiction, but others have decided it is a separate case.
-
A rational number is any one that can be represented by a fraction, like:$$\frac{2}{3}\mbox{, }\frac{57}{21}\mbox{ or }\frac{3}{3}$$
- Pythagoras (c.569-475 BCE) founded a society which continued well into the 5th century.
- In-commensurable means that there is no common measure between two given lengths.In this case, a side of a square and its diagonal cannot be measured exactly in the same units, or fractions of the unit.
- In this case, a side of a square and its diagonal cannot be measured exactly in the same units, or fractions of the unit. See Pedagogical Notes and Questions 1(c) .
- Another name for these numbers is 'surds'.
- For details on Euclid see D.E. Joyce's commentary at weblink EUC
- See Netz and Noel (2007) for the most startling recent discoveries about Archimedes.
- In this kind of projection, the lengths of lines and the shapes of curves change, but the order in which points are connected, remains the same.The term invariant refers to properties that remain the same under some kind of transformation.
- The original conjecture by Descartes was investigated by Euler in 1758 when attempting to classify polyhedra.
- The publication of Lakatos' original thesis in 1961 was a major factor in the development of Investigations in school mathematics.
- Iso-morphic means the 'same shape'. Isomorphic crystals of chemicals with similar composition can grow on each another, as often seen in the school science laboratory.
- See Robin Wilson's Four Colours Suffice (2002). This is the history of the map colouring problem first proposed by a student of Augustus De Morgan in 1852. The first proof in 1976 counted 1,936 different maps, but after re-testing the program and discovering mistakes, by 1994 the number had been reduced to 633. There are still some people who doubt the result.
- Known also as Bhaskara II or 'Bhaskhara the Teacher'.
- In the early 20th century, Hardy, and others at Cambridge found many of the results of the brilliant Indian mathematician Ramanujan (1887-1920) difficult to understand because the proof methods were unlike anything they had seen before. Even today, mathematicians are still discovering important new results from the work of Ramanujan.
References
Berggren, J. L. (2003) Episodes in
the Mathematics of Mediaeval Islam New York, Berlin. Springer
(original 1986)
D'Amore, B. (2005) Secondary school
students' mathematical argumentation and Indian Logic (Nyaya).For
the Learning of Mathematics 25 (2) July 2005 (26, 32)
Datta, B. ; Singh, A. N.(1935)
History of Hindu mathematics, a source book. Lahore,: Motilal
Banarsi Das. (Reprinted by Bharatiya Kala Prakashan, Delhi)
Dauben, J.W. (2007) Chinese
Mathematics in Katz, V. J. (ed.) Sourcebook (187-384)
Lakatos, I. (1976) (Eds. Worrall,
J. and Zahar, E.) Proofs and Refutations: The Logic of Mathematical
Discovery London. Cambridge University Press
Kanigel, R. The Man Who Knew
Infinity: A Life of the Genius Ramanujan Johns Hopkins Univerity
Press
Katz, V. J. (2007) (ed.) The
Mathematics of Egypt, Mesopotamia, China, India and Islam: A
Sourcebook. Princeton and Oxford. Princeton University Press
Keller, Agathe (2005) Making
diagrams speak, in Bhskara I 's commentary of the Aryabhatiya.
Historia Mathematica 32: 275-302.
Keller, Olivier. (2006) Une
Archeologie de la Geometrie (An Archeology of Geometry) Paris.
Vuibert
Martzoff, J-C. (1987) A History of
Chinese Mathematics Berlin, New York. Springer
Newton, Isaac. (1745) Sir Isaac
Newton's Two Treatises on the Quadrature of Curves, and Analysis by
Equations of an infinite Number of Terms explained: London John
Stewart
Netz, R. and Noel, W (2007) The
Archimedes Codex. London. Weidenfeld & Nicolson
Plofker, K. (2007) Mathematics in
India in Katz, V. J., Sourcebook (385-514)
Li Yan and Du Shiran (1987) Chinese
Mathematics : A Concise History. John N. Crossley, J.N. and Lun,
A.W.C. Oxford. Oxford Science Publications.
Watson, A. and Mason, J. (1998)
Questions and Prompts for Mathematical Thinking Derby. Association
of Teachers of Mathematics
Wilson, R. (2002) Four Colours
Suffice: How the Map Problem was Solved London. Penguin Books
Web
Links
Non-Euclidean Geometry (NEG)
http://www-history.mcs.st-andrews.ac.uk/HistTopics/Non-Euclidean_geometry.html
MacTutor has many useful pages on
Indian and Chinese mathematicians http://www-history.mcs.st-and.ac.uk/history/
For India and China, there are
resources on the French website: http://www.dma.ens.fr/culturemath/index.html
. The outstanding scholars here are Agathe Keller for India and
Karine Chemla for China. There is very little from these two
researchers available in English at the moment.
Snezana Lawrence of Simon Langton
School in Kent offers many ideas for teaching mathematics using
history on her website: http://www.mathsisgoodforyou.com/
She has also set up a History
section on the NCETM website at: http://www.ncetm.org.uk/ and then
search for the History of Mathematics Community

