Skip over navigation
We recieved two very different interpretations of these numbers. Do theyconvince you?
James and Ryan said that
We think that the numbers are two of a pair of pythagorean triples $(a, b, c)$, so that
$$
a^2+b^2=c^2
$$
In each case the third number is
$$120, 3456, 4800, 13500, 72, 360, 2700, 960, 600, 6480, 60, 2400, 240, 2700, 90$$
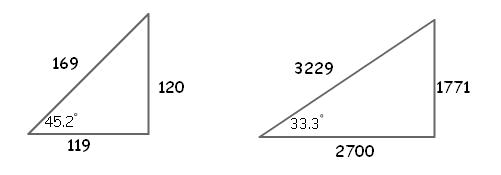
We wondered why these numbers had been picked in this order, but then found out that they are arranged in order of decreasing angle of the triangle. So, the first row is a (119, 120, 169) triangle which has an angle of $45.2^\circ$ and the last but one has an angle of $33.3^\circ$.
Our hypothesis shows that the errors are in rows 2, 9, 13, 15. These should read
4825, 11521
541, 481
25921, 161
53, 106
The Babylonians might have used these numbes to help to build things.
Michael writes suggesting that the numbers are related to astronomical measurements
The numbers are the measurements of time.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Babylon Numbers
Age 11 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We recieved two very different interpretations of these numbers. Do theyconvince you?
James and Ryan said that
We think that the numbers are two of a pair of pythagorean triples $(a, b, c)$, so that
$$
a^2+b^2=c^2
$$
In each case the third number is
$$120, 3456, 4800, 13500, 72, 360, 2700, 960, 600, 6480, 60, 2400, 240, 2700, 90$$
We wondered why these numbers had been picked in this order, but then found out that they are arranged in order of decreasing angle of the triangle. So, the first row is a (119, 120, 169) triangle which has an angle of $45.2^\circ$ and the last but one has an angle of $33.3^\circ$.
Our hypothesis shows that the errors are in rows 2, 9, 13, 15. These should read
4825, 11521
541, 481
25921, 161
53, 106
The Babylonians might have used these numbes to help to build things.
Michael writes suggesting that the numbers are related to astronomical measurements
The numbers are the measurements of time.
- The number 3541 which is the equivalent of 10 lunar years with just 2 leap days.
- That leads to 4961 which compares to 14 lunar years.
- The number 8161 is the equivalent of 23 lunar years with 11 leap days.
- Is the 10 in the third row intended as leap days?
- 1771 equates to 5 lunar years.
- The number 2929 is practically identical to 8 solar years at 2922 days.
- That 8 year period is also 13 orbits of Venus.
- It is also 5 orbits of the Synodic cycle at 2920 days.
- 4961 is also 22 orbits of Venus making it a common target with 14 lunar years.
- 18,541 equates to 27 orbits of mars.
- The total of the second column at 57613 equates to 99 synodic cycles while the totals of the three columns at 116,798 equates to 200 synodic cycles and the totals of column 1 and 3 equates to 101 synodic cycles.
- There are more synodic cycles evident with the addition of numbers e.g. 2291 + 3541 = 5832 or 10 synodic cycles in 16 years. (+ the 7 as leap days)
- But what about 1679? It equates exactly to one orbit of the Asteroids which were only discovered in 1801 with the aid of a telescope?
- The number 25,921 is just one above the cycle of the Zodiac at 25,920 years, so the numbers are neutral to represent days or years i.e. = 71 solar years.
You may also like
Divided Differences
When in 1821 Charles Babbage invented the `Difference Engine' it was intended to take over the work of making mathematical tables by the techniques described in this article.

