Skip over navigation
By Henry Kwok
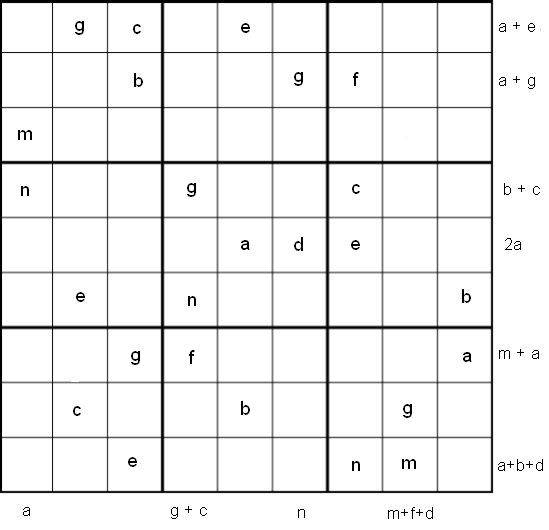
All-variables Sudoku
Age 11 to 18
Challenge Level 
By Henry Kwok
Rules of All-Variables Sudoku
Like the standard sudoku, this sudoku variant has three basic rules:- Each column, each row and each box (3x3 subgrid) must have the numbers 1 through 9.
- No column, row or box can have two squares with the same number.
- In addition to the above two basic rules, the puzzle can be solved by finding the values of the 9 given variables in the squares of the 9x9 grid.
At the bottom and right side of the 9x9 grid are groups of
similar variables. Each set of variables is the sum of a column or
row of variables in the 9x9 grid. A set of 10 equations can be
formed from the columns and rows of variables.
For example, in the first and fourth columns beginning from
the left of the 9x9 grid, we can form the following
equations:
m + n = a
g + n + f = g + c
In the second and last rows beginning from the top of the 9x9
grid, the following equations can be formed:
b + g + f = a + g
e + n + m = a + b + d
After solving all the equations, the puzzle is solved by the
usual sudoku technique and strategy.
You may also like
Real(ly) Numbers
If x, y and z are real numbers such that: x + y + z = 5 and xy + yz + zx = 3. What is the largest value that any of the numbers can have?
