Skip over navigation

Logic Block Collections

Age 5 to 7

Challenge Level Yellow star

Logic Block Collections

Have you seen a set of Logic Blocks? There are different shapes, different colours and two different sizes.

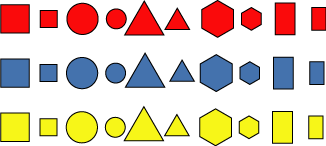
I have been collecting some Logic Blocks that go together in a set because something about them is the same. It could be something about their shape or their size or their colour.

What do you think is the same about these two? What other Logic Blocks do you think go with them in the set?

Scroll down to find some more shapes in the set.

Here are the rest of the set.

What others could it have been?

Here are two shapes from another set.

What do you think is the same about these two?
What other Logic Blocks do you think go with them in the set?

Scroll down to find some more shapes in the set.

Here are some more of the set.

What others do you think go with them? There are ten of them altogether.

Now you can make your own sets of shapes. If you don't have any blocks of your own, you could print off and cut up the shapes on this sheet.

Why do this problem?

This problem gives children a set of objects to sort with very distinct criteria which means that they will have opportunities to develop appropriate mathematical language. This is also a chance for children to make hypotheses and then alter them once more information is available.

Possible approach

If possible, children should have a set of Logic Blocks to handle and sort before starting this activity. Encourage them to describe features of the blocks, for example, you could ask one child to describe a shape for the others to guess.

Begin by revealing only the starting shapes and ask pairs of children to come up with suggestions for which other shapes could go with them. Invite pairs to share their ideas with the whole group - you could make a note of each idea. The important thing is to encourage learners to give clear reasons for the groupings they have made - it is only when more information is given that we can be more certain of the correct set.

The problem does not differentiate between the different thicknesses in the Logic Blocks so that one set can be shared between two groups of children. If real Logic Blocks are not available, this coloured sheet can be printed out and cut out. If a photocopiable sheet is more suitable this can be coloured by the children before being cut up.

As a plenary, you could ask a pair to come up to choose two shapes which fit a criterion. Other members of the group could come up and add another shape into the set and the pair move it if it doesn't fit with their criterion. You could carry on in this way until the set has been correctly described.

Key questions

What is the same about these two blocks?

What others could go with them?

Is there anything else that is the same about these two blocks?

Which others would go with them this time?

Possible extension

Learners could be challenged to draw their own shape/s which fit the set.

Possible support

Some children might benefit from some simpler sorting activities to being with, for example finding all the squares, then all the large shapes of one colour etc.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Logic Block Collections

Logic Block Collections

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

Tangrams

Three Squares

Chain of Changes