Skip over navigation
We could be making some car journeys between these towns and so here is a chart giving us some information about distances and times.
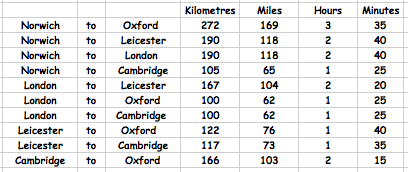
These numbers show us direct routes. But now, suppose we go on journeys involving three or four cities.
For example, we could go from Norwich to Oxford but go through Cambridge on the way.
Or, we could go from London to Leicester but go through Oxford on the way.
What other journeys involving three or four cities can you find?
When you have some of these answer these questions:
1. What is the total distance of your journey in kilometres?
2. How many minutes long is your journey?
3. How much longer (in terms of time) is the journey when passing through another city or other cities along the way compared with the direct journey between the starting city and the final destination?
Now you could try and find the longest route (in terms of distance) for visiting all five cities.(We might decide that we will only visit each city once.)
What about the shortest route for visiting all five cities?
How much longer does it take to travel the longest route compared with the shortest route?
Lengthy Journeys
Age 7 to 11
Challenge Level 
Here is a simple map showing the positions of five cities in England:
We could be making some car journeys between these towns and so here is a chart giving us some information about distances and times.
These numbers show us direct routes. But now, suppose we go on journeys involving three or four cities.
For example, we could go from Norwich to Oxford but go through Cambridge on the way.
Or, we could go from London to Leicester but go through Oxford on the way.
What other journeys involving three or four cities can you find?
When you have some of these answer these questions:
1. What is the total distance of your journey in kilometres?
2. How many minutes long is your journey?
3. How much longer (in terms of time) is the journey when passing through another city or other cities along the way compared with the direct journey between the starting city and the final destination?
Now you could try and find the longest route (in terms of distance) for visiting all five cities.(We might decide that we will only visit each city once.)
What about the shortest route for visiting all five cities?
How much longer does it take to travel the longest route compared with the shortest route?
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.