Spot the Difference

Chieh Lung from Kolej Tuanku Jaafar school made a good start on this:

$x + y -1 =0$ and $x + y = 1$ are the same equation, they give the top line, running through $(1,0),(0.5,0.5)$ and $(0,1)$.
$x + y = 0$ is the lower line, running through the origin.
The rest of the equations must just be multiples of these.

$(x+y-1)(x^2+y^2)=0$. The solutions of this are like solving a quadratic equation, when solutions are when at least one of the brackets is equal to zero. Here the first bracket is the top line, and the second only has solutions at $(0,0)$ as we are in the real numbers.

$x^3 + 3xy + y^3 = 1$. This must also be a product of the lines and points. But I cannot find them.

Good start Chieh, Adam finished off your working;

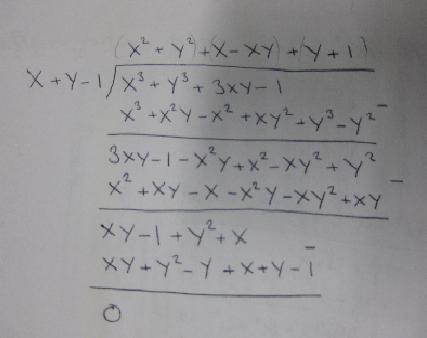
So you can see that $x^3 + y^3 +3xy -1 = (x +y)(x^2+y^2+x+y-xy+1)$
To see if $x^2+y^2+x+y-xy+1$ has any solutions I wrote it as a quadratic in $x$ and used the quadratic formula.

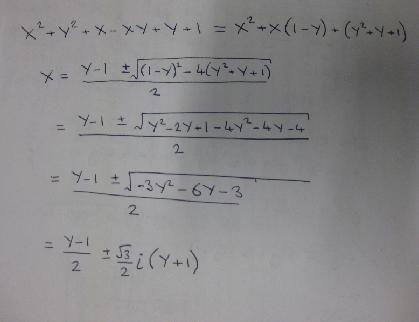
As you can see the solutions are imaginary, they contain an $i$. So The second bit can only equal zero at specifc points, not a whole line. So another point at $(-1,-1)$.
So the graphs of these six functions either lie on two lines, or have single discrete solutions, and so the effect of just two visable lines is achieved.

This effect could be created many times by choosing two lines, and then multiplying them by points (say $x^2+y^2=0$).