Skip over navigation

So many things that we look at in Maths have a regular steady pattern that we can find and explain. For a change, let's look at things that happen more randomly.
We sometimes throw dice, toss a coin or use a rhyme to choose something at random. In this problem, we'll have a look at something a bit different - birds in the garden.
So, let's do some bird watching in our garden - at home or at school. People who do a lot of bird watching keep a chart to record which birds visit their gardens. The chart might look like this;
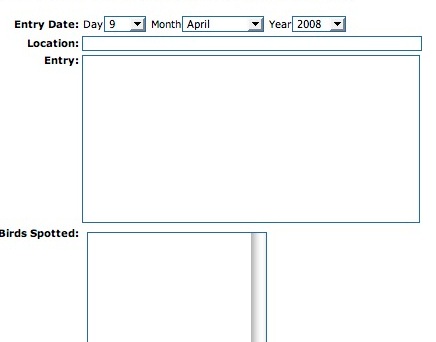
You might want to use a similar chart over a period of, for example, a week. Or you could just do it for one day and note the time.
Once you have a few items recorded, it would be good to have a discussion about the information you have recorded and to ask yourself some questions about it.
How many birds of a particular type did you record on each day (or each hour)?
Did you see the same type of birds at specific times of the day?
How may different types of birds did you see each day (or each hour)?
You will be able to think of many other questions too.
Are you able to see any patterns in the information you collected or do the sightings of birds appear to be quite random?
If you do find any patterns, can you try to explain why, or at least have an idea of the reason?
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Birds in the Garden
Age 5 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Birds in the Garden

So many things that we look at in Maths have a regular steady pattern that we can find and explain. For a change, let's look at things that happen more randomly.
We sometimes throw dice, toss a coin or use a rhyme to choose something at random. In this problem, we'll have a look at something a bit different - birds in the garden.
So, let's do some bird watching in our garden - at home or at school. People who do a lot of bird watching keep a chart to record which birds visit their gardens. The chart might look like this;

You might want to use a similar chart over a period of, for example, a week. Or you could just do it for one day and note the time.
Once you have a few items recorded, it would be good to have a discussion about the information you have recorded and to ask yourself some questions about it.
How many birds of a particular type did you record on each day (or each hour)?
Did you see the same type of birds at specific times of the day?
How may different types of birds did you see each day (or each hour)?
You will be able to think of many other questions too.
Are you able to see any patterns in the information you collected or do the sightings of birds appear to be quite random?
If you do find any patterns, can you try to explain why, or at least have an idea of the reason?
Why do this problem?
This activity can be used to draw children's attention to the idea that some things appear to happen randomly. At the highest level, it can be used as a way to encourage pupils to reflect on differences between pure number patterns (for example in investigations such as Investigating Pascal's Triangle or Doplication ) and patterns in real data.
Possible approach
You could introduce this activity by inviting children to predict whether they think there will be any patterns in the collected data. Keep these hypotheses listed on the wall somewhere so you can refer back to them later. This will also help when it comes to asking questions about the information.
Involve the whole class in designing some sort of recording sheet or chart to begin with - this could be incorporated into an electronic database. Once the timescale has been agreed upon, you can allot parts of the task to different groups of children so that it is a collective effort. You might have an ongoing wall chart which is added to as data is collected.
When it comes to looking at the information, encourage children to investigate as many ideas as they can. Emphasise that they should be able to describe any patterns they notice and begin to suggest reasons for the patterns.
Which of their original hypotheses seemed to be right and which did not?
What would they need to do in order to be more certain?
Could they describe any of the birds' sightings as random? Why?
Key questions
What have you noticed?
Can you find any patterns?
Are you able to suggest why those patterns occurred?
Would you describe any of the data as random? Why?
Possible extension
Some children might like to extend the activity by practically carrying out investigations to test whether the patterns they have noticed continue and whether other patterns emerge.
Possible support
Visit http://www.rspb.org.uk/ where you can find practical advice and contribute to nationwide wildlife surveys (in the UK).
You may also like
Two and One
Terry and Ali are playing a game with three balls. Is it fair that Terry wins when the middle ball is red?
Three Ball Line Up
Use the interactivity to help get a feel for this problem and to find out all the possible ways the balls could land.
Florence Nightingale - the Compassionate Mathematician
Florence Nightingale may be well known for her role as a nurse, but she was also an excellent mathematician, collecting and analysing data to help improve hospital conditions.

