Skip over navigation
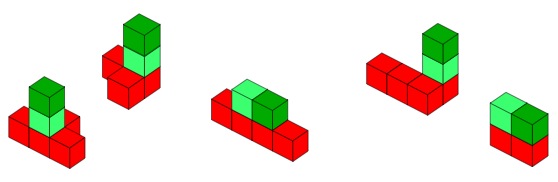
This is all about putting green cubes on top of red cubes with some simple rules.
1) The red cubes must be touching the floor (or table top etc.).
2) The green cubes must not be touching the floor.
3) All the cubes are interlocking cubes so they can only be joined square face to square face.
4) The green cubes are next to each other.
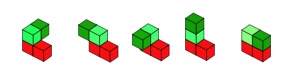
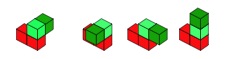
So, your first challenge is to find the possibilities with two green on three red cubes.
When you've done that, what can you say about the results you might get for having two on four?
Can you give some reasons for your predictions?
How about testing whether they were right?



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cubes Here and There
Age 7 to 11
Challenge Level 






This is all about putting green cubes on top of red cubes with some simple rules.
1) The red cubes must be touching the floor (or table top etc.).
2) The green cubes must not be touching the floor.
3) All the cubes are interlocking cubes so they can only be joined square face to square face.
4) The green cubes are next to each other.

In the pictures above, I used two red cubes and two green cubes, but in different shades of green so as to help me with the method I used to find all the possibilities. You might do it some other way.
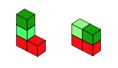
You have to look carefully for answers that are really the same - just turned around. So these "other" ones are really the same as the some of the five above.

Some of these models have green cubes that "hang-over" and for this challenge, we'll decide not to use these. (But you could make the activity harder by including them, if you want!). We'll only use these;

So, your first challenge is to find the possibilities with two green on three red cubes.
When you've done that, what can you say about the results you might get for having two on four?
Can you give some reasons for your predictions?
How about testing whether they were right?
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Tea Cups
Place the 16 different combinations of cup/saucer in this 4 by 4 arrangement so that no row or column contains more than one cup or saucer of the same colour.
Tiles on a Patio
How many ways can you find of tiling the square patio, using square tiles of different sizes?

