Dilution Series Calculator

A solution to an interactive of this sort is best done with a worked example:



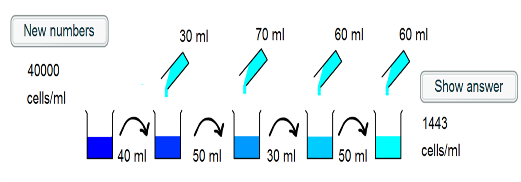
1) The intial beaker contains 40000 cells/ml. 40ml of this is taken, and so there are $40000 \times 40 = 1.6 \times 10^6$ cells placed into the second beaker.

2) 30ml of water is added to the second beaker, such that the cells are in a volume of 70ml. The concentration is now $\frac{1.6 \times 10^6}{70} =2.29 \times 10^4$ cells/ml.

3) 50ml of this suspension is taken and placed into the third beaker, and so $2.29 \times 10^4 \times 50 = 1.14 \times 10^6$ cells are transferred.

4) A further 70ml of water is added, such that the cells are in a 120ml suspension. This corresponds to a concentration of $\frac{1.14 \times 10^6}{120} = 9.52 \times 10^3$ cells/ml.

5) 30ml of the suspension is transferred, which corresponds to $30 \times 9.52 \times 10^3 = 2.86 \times 10^5$ cells.

6) 60ml is added to the fourth beaker, and so the cells are in a 90ml volume. The concentration is hence $\frac {2.86 \times 10^5}{90} = 3175$ cells/ml.

7)50ml of the suspension is transferred to the final beaker, corresponding to $ 50 \times 3175 = 1.59 \times 10^5$ cells

8) 60ml more water is added to give a final volume of 110ml. Thus the final concentration is $\frac{1.59 \times 10^5}{110} = 1443$ cells/ml


Of additional interest is a general rule.

$n_f$ is the final cell concentration
$n_i$ is the initial cell concentration
$V_1, V_2, V_3, V_4$ are the volumes transferred to the second, third, fourth and fifth beakers respectively
$V_a, V_b, V_c, V_d$ are the volumes added to the second, third, fourth and fifth beakers respectively.

Thus,

$$n_f = \left(\frac{\left(\frac{\left(\frac{\left(\frac{n_i \times V_1}{V_1 +V_a}\right) \times V_2}{V_2 + V_b}\right) \times V_3}{V_3 + V_c}\right)\times V_4}{V_4 + V_d}\right)$$
$$ = \frac{n_iV_1V_2V_3V_4}{(V_1 + V_a)(V_2 + V_b)(V_3 + V_c)(V_4 + V_d)}$$

Thus, the dilution series calculation reduces to multiplication of fractions.