Exact Dilutions

There are three parts to this question, which require increasing amounts of thought. However, all are based on the standard mathematics of dilutions.

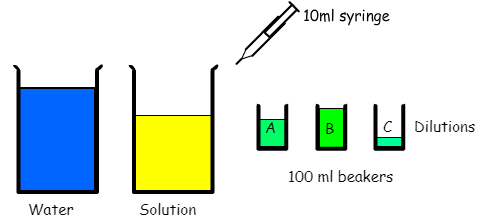
You are provided with a large quantity of a solution of a chemical at a standard concentration and a large supply of water with which to dilute the solution. You have three 100ml beakers in which to mix dilutions and a 10ml syringe to transfer fluids from the large beakers to the small beakers or between the small beakers. The 10ml syringe can only measure exactly 10mls.

Part 1:
For certain applications you require non-standard dilutions. Try to use the three beakers and syringe to create a quantity of dilutions in each of these cases (in increasing order of complexity)

1. 1/3
2. 1/7
3. 1/18
4. 5/12
5. 29/35
6. 71/882
    

Part 3:
I mix a dilution with a concentration $c_A$ in the first beaker and a smaller concentration $c_B$ in the second beaker. I pour some liquid (unmeasured amounts) from beakers A and B into beaker C to make a new dilution with concentration $c_C$. Use common sense to understand and algebra to prove that $$c_A> c_C> c_B$$

On a scrap of paper I found this method for making a 1/13 dilution using the above configuration of beakers:

1. Fill beaker A with 100ml of water.
2. Put 10ml of solution and 20ml of water into beaker B.
3. Roughly fill beaker B with fluid from beaker A.
4. Roughly fill beaker A with fluid from beaker B.
5. Repeat steps 3. and 4. 10 times.

Can you extend this method to produce a way of mixing a 1/23 dilution using the above configuration of beakers?