Skip over navigation
By Henry Kwok
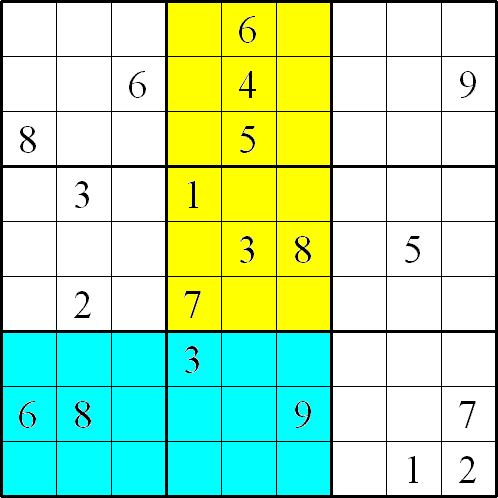
As in a standard Sudoku, the object of the puzzle is to fill in the whole 9x9 grid with numbers 1 through 9 so that each row, each column, and each of the nine 3x3 squares must contain all the nine different numbers 1 through 9.
There are two coloured "islands" in the 9x9 grid. Within each "island" there are two extra rules to apply:
Colour Islands Sudoku
Age 11 to 14
Challenge Level 
By Henry Kwok
Rules of Colour Islands Sudoku
As in a standard Sudoku, the object of the puzzle is to fill in the whole 9x9 grid with numbers 1 through 9 so that each row, each column, and each of the nine 3x3 squares must contain all the nine different numbers 1 through 9.
There are two coloured "islands" in the 9x9 grid. Within each "island" there are two extra rules to apply:
- no two diagonally adjacent cells can contain the same number
- EVERY 3x3 square within the islands must contain the numbers 1 through 9.
For example the cell (5,3)
contains the number 5 so the cell (6,4) in the yellow island cannot
contain a 5 because it is diagonally adjacent to (6,4) - being to
the right and down one.
The 9x9 grid with corners at C4R3,
C4R5, C6R5 and C6R3 must contain all the digits 1 to 9.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Tea Cups
Place the 16 different combinations of cup/saucer in this 4 by 4 arrangement so that no row or column contains more than one cup or saucer of the same colour.
Counting on Letters
The letters of the word ABACUS have been arranged in the shape of a triangle. How many different ways can you find to read the word ABACUS from this triangular pattern?