Find the Difference

Thank you to everybody who sent in their solutions to this problem. Lots of children sent us one or two solutions, but only a few children managed to find every solution. Well done to all of you!

Dhruv from The Glasgow Academy in Scotland sent in these two solutions along with some reasoning about where the 5 and 6 could go:

That reasoning is really clear, Dhruv - you've convinced me that 6 has to be on the bottom row and that 5 can't go at the top.

We received a lot of solutions from the children at St Helen's C of E School in England. Sonny, Reuben and Rio found a similar solution to one of Dhruv's, and they explained their process:

       1             This is the correct solution.
   4     3
6     2     5
First, we tried 1 at the top.Then we put 3 and 2 on the middle section. Then we put 6 and 4 at the bottom and knew that it was wrong.
On our 2nd try we put 1 at the top, 4 and 3 in the middle and 6, 2 and 5 at the bottom which was right!
6 cannot be put in the top or middle sections because it is the highest number.
5 can only be in the bottom or middle sections.

Ralph found a different solution and noticed something about where the 3s could go:

      2
   5    3
6    1    4

I knew that 6 had to be at the bottom because there was no bigger number to make a difference.
1 was the first number I tried next to 6 and it worked!
I knew 3 couldn't go next to 6 because we would need two 3s.

Amelia-May, Amélie and Joanne found another new solution. They noticed the same thing as Ralph, and also noticed something about the 4 and 2:

We found out that 6 could only be placed in the bottom row because it was the largest number and it couldn't be the difference between any other numbers.
Our 5th and 6th attempts were the only ones that were effectively successful.
Numbers that we found couldn't go together were 2 and 4 because there is a difference of 2 and there was only one 2 on top of that 3 and 6 because the difference is 3 and again there is only one of each number.
We found 2 solutions:

       1
   4     3
6     2      5

and

       3
   1      4
5     6      2

Thank you all for sharing your ideas with us, and thank you as well to Albie, Adam, Riley, Sam, Olivia, Tommie, Frances, Lucy, Rosie and Ophelia who all sent in very well-reasoned solutions. We also received some similar solutions from: Nivaan Haluvaagilu from Ekya School JP Nagar in India; all the children at Cromwell Community College Primary Phase in the UK; May, Mia, Joanna and Jolene from Falcons School for Girls; and Micah, Ruth, Blythe and Khalil from Bay Vista Fundamental in the USA.

Alba from Barton C of E School in Cambridge, UK managed to find every possible solution. Alba said:

I used my number bonds.
I used counters to help.
You can’t put 6 and 3 together because you make 6 as 3 + 3
6 can't go up high because it’s the biggest number.
I highlighted the triangles that matched and it helped me to find the missing one.

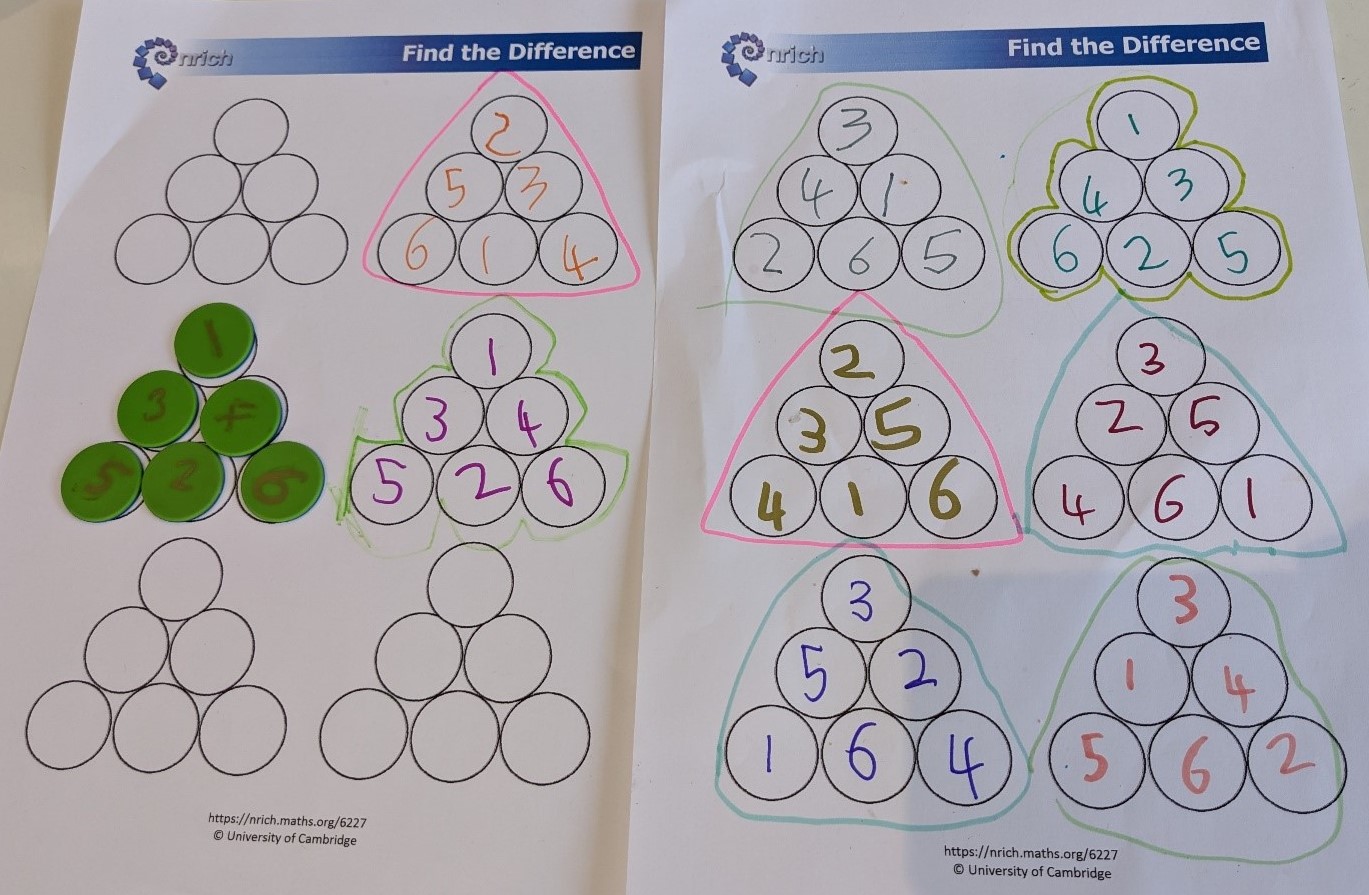
Well done, Alba! This is an excellent example of how we can work systematically to find a solution that we've missed out. Can you see how Alba has decided which triangles 'match'?

We also received a full solution from Vansh, Eshaan, Vraj, Rishaan, Samaira, Renah, Udit, Uday, Viha, Gowri, Arya, Krishna, Rivaan, Miraya and Hiren at Ganit Kreeda, Vicharvatika in India. Their observations were: 

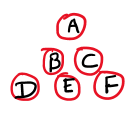
6 cannot go in the topmost two rows as 6 being the biggest number it is not possible to find 2 numbers from 1 to 6 whose difference is 6. That means 6 can occupy only boxes in the bottom row.

5 cannot come at the topmost layer as we cannot use 6 in the second row.

4 cannot come at the topmost square as the only way to get 4 is by 5-1 in the 2nd row. To get 5 in the second row, the only way is 6-1. As we cannot repeat the numbers (1), we cannot use 4 at the top.

Only smallest 3 numbers (first 3 numbers) can come at the top.

Based on our observations we made a table as follows:

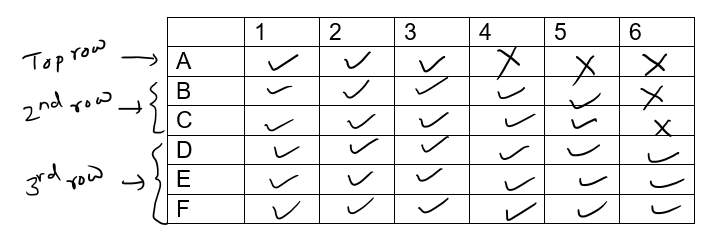
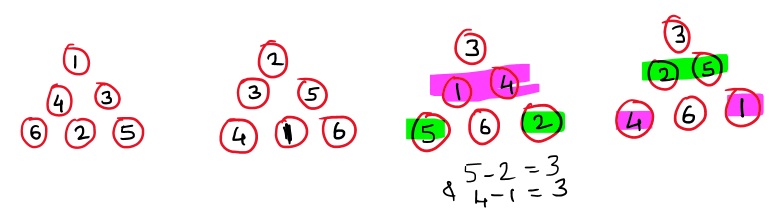
Kids analysed the solution from the 3-layer pyramid with 3 at the top.

They noticed that by changing the positions of 1 and 4 with 5 and 2, we can get these 2 different solutions.

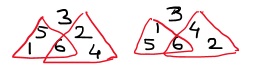
Rishaan beautifully explained the reason.

4-1 = 5-2 =... so we can change their positions.

Also, 6-1=5 & 6-5=1 and 6-4=2 & 6-2=4

We can change their relative positions.

Well explained, Rishaan, and well done to all of you for your hard work on this. To see more ideas from this group, including some algebraic reasoning from Samaira, take a look at Ganit Kreeda's full solutions.