Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Venn Diagrams



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Venn Diagrams
Take a look at the interactivity below. Before you try anything, have a think about these questions:What do you see?
What do you wonder?
We call this way of sorting information a Venn diagram (named after the mathematician John Venn).
Can you drag the numbers from 1 to 30 into their correct places in the Venn diagram?
How do you know where to put each number?
Here is another one for you to try.
How do you know where to put each number this time?
If you would prefer to work away from a screen, you could print off these sheets, which have a copy of each Venn diagram on them.
Here is a screenshot (a picture) of the interactivity, but the labels of the Venn diagram are missing.
What could the labels be?
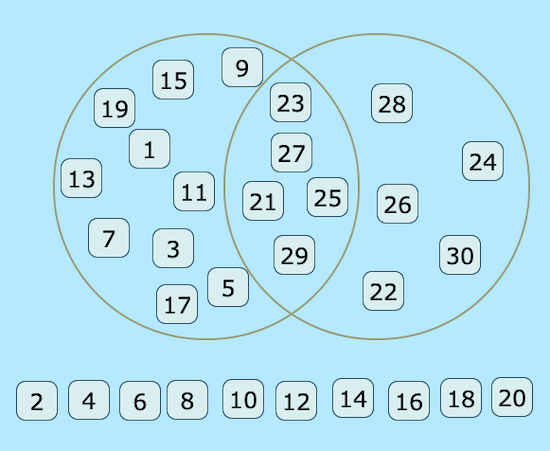
Here is another version of the interactivity for you to try.
What do you notice this time?
Can you explain your 'noticings'?
If you click on the purple cog of the interactivity, you can change the settings and create your own Venn diagrams for someone else to complete.
Why do this problem?
This problem provides an opportunity for children to become familiar with Venn diagrams, whilst reinforcing knowledge of number properties. Placing numbers in a Venn diagram requires children to consider more than one property of a number at the same time. This problem is also a good context in which to encourage learners to articulate their reasoning.
Possible approach
This activity featured in an NRICH Primary webinar in March 2021.
You could introduce the task by projecting the first version of the interactivity using an interactive whiteboard. Without doing anything at all, invite learners to consider what they see and what they wonder.
After giving some time for children to talk in pairs, bring them together to share their thoughts and any questions they have. Through this whole group discussion, you can draw out the features of Venn diagrams and you may like to invite some children to come and drag a number to the correct place, and ask someone else to explain why that is correct. Equally valid is to ask someone to drag a number to an incorrect cell, again asking for an explanation from a different learner.
You can set the children off on the task, either using the interactivity if you have access to tablets/computers, or on paper. This sheet contains copies of the first two diagrams in the problem. If children work in pairs it will encourage them to construct mathematical arguments to convince each other where on the diagram each number belongs. Explaining out loud in this way often helps to clarify thinking and will give a purpose for accurate use of mathematical vocabulary.
You could listen out for misconceptions or disagreements to share in a plenary so that all children become involved in the reasoning. You may also like to look at the image of the diagram with missing labels in the plenary. Give learners time to talk in their pairs before inviting a few to share their solution. You will find that different pairs have 'homed in' on different numbers to help them solve this part of the task, therefore it is worth hearing from a few so that more than one strategy is shared.
You can end the lesson with the final interactivity. What do they notice? You may need to encourage the class to start dragging numbers into the correct places before they realise that there won't be any numbers in the intersecting region in the middle. Why not?
Clicking on the purple cog of the interactivity allows you to change the settings so you can tailor the labels and sets of numbers to suit your learners.
Key questions
Possible extension
Children can create their own Venn diagrams for others to complete. Alternatively, you could challenge them to create Venn diagrams which have certain criteria e.g. an empty intersection (like the final example in the problem); all items in the intersection; three overlapping sets etc.
Possible support
Some learners might find it easier to collect numbers with a certain property, for example, even numbers or numbers less than 10, in single circles. Then they can look at those that should go in both circles.
You may also like
Number Round Up
Arrange the numbers 1 to 6 in each set of circles below. The sum of each side of the triangle should equal the number in its centre.
Grouping Goodies
Pat counts her sweets in different groups and both times she has some left over. How many sweets could she have had?

