Skip over navigation
By Henry Kwok
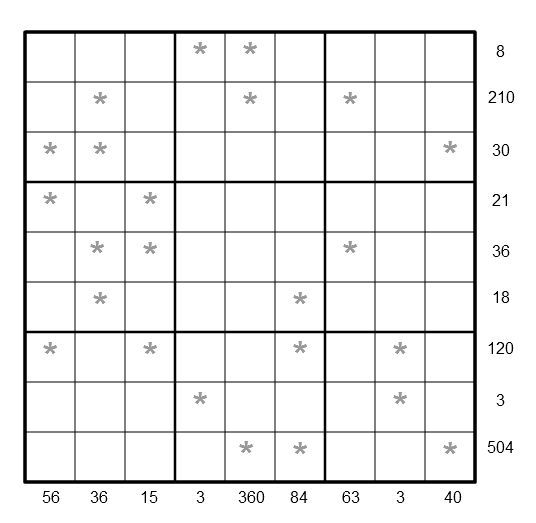
LCM Sudoku II
Age 11 to 18
Challenge Level 
By Henry Kwok
Rules of LCM Sudoku
Like the standard sudoku, this sudoku variant has the basic rule:
- Every row, every column and every $3\times 3$ box in the grids contains the digits $1$ through $9$.
The puzzle can be solved by finding the values of the unknown digits (all indicated by asterisks) in the squares of the $9\times 9$ grid. At the bottom and right side of the $9\times 9$ grid are numbers, each of which is the Least Common Multiple (LCM) of a column or row of unknown digits marked by asterisks.
Altogether $18$ Least Common Multiples of $9$ columns and $9$ rows of unknown digits are given as clues for solving the puzzle.
As an example, the LCM of $3$, $9$, $6$, $4$, $2$ and $1$ is $36$. In the puzzle, the LCM of the four unknown digits in the second column beginning from the left of the $9\times 9$ grid is $36$, while the LCM of the four unknown digits in the seventh row beginning from the top of the $9\times 9$ grid is $120$.
After finding the values of all the unknown digits, the puzzle is solved by the usual sudoku technique and strategy.
You may also like
Real(ly) Numbers
If x, y and z are real numbers such that: x + y + z = 5 and xy + yz + zx = 3. What is the largest value that any of the numbers can have?
