Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Published 2008 Revised 2021
Geometry: A History from Practice to Abstraction
1. Ancient and Classical Geometries

Aristotle (384-322) BCE

Euclid of Alexandria
(325-265)
The first three postulates are about what can be done, the next one about equality of right angles and the final statement uses the sum of two right angles to define whether two lines meet:
- Draw a straight line from any point to any other point.
- Produce (extend) a finite straight line continuously in a straight line.
- Describe a circle with any centre and distance.
- All right angles are equal to each other.
- If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, then if the two lines are produced indefinitely, they will meet on that side where the angles are less than the two right angles.
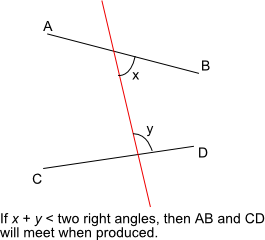
- Given a line and a point not on the line, it is possible to draw exactly one line through the given point parallel to the line.

Playfair's Axiom

John Playfair (1748-1819)
Abul Wafa al-Buzjani (940-998)
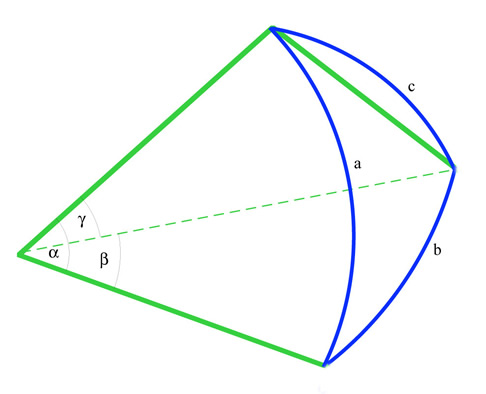
Spherical Triangle
Omar Khayyam (1048-1131)

Omar Khayyam (1048-1131)
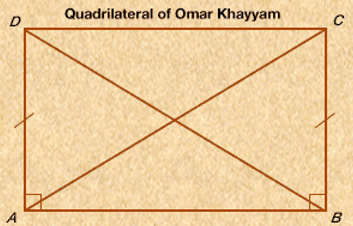
Omar Khayyam Quadrilateral
Nasir al-Din al-Tusi (1201-1274)

Nasir al-Din al-Tusi (1201-1274)
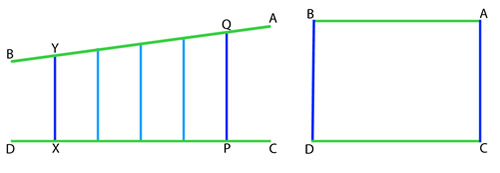
Al-Tusi's diagram

Al-Tusi's original diagram
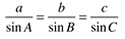
Plane triangle sine rule
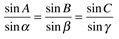
Spherical triangle sine rule
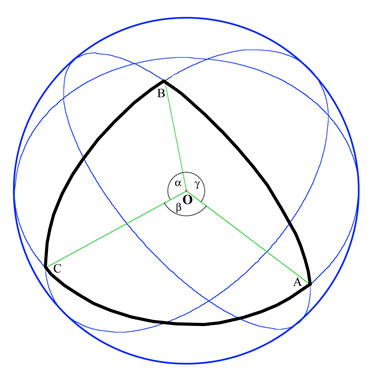
Great Circles Triangle
2. Renaissance and Early Modern Developments
The Painters' Perspective

Leone Battista Alberti (1404-1472)
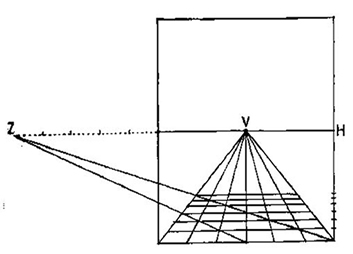
Alberti Perspective Construction

Piero della Francesca (1412-1492)
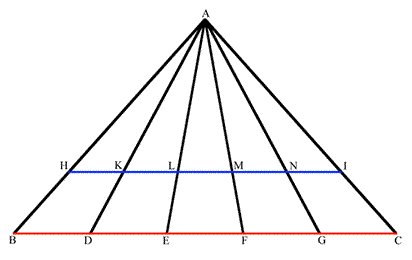
Piero Euclid VI, 21 diagram
Other famous artists improved on these methods, and in 1525 Albrecht Durer (1471-1528) produced a book demonstrating a number of mechanical aids for perspective drawing.

Durer "Reclining woman" perspective picture

Albrecht Durer (1471-1528)
Desargues and Projective Geometry
In 1639, Girard Desargues (1591-1661) wrote his ground-breaking treatise on projective geometry. He had earlier produced a manual of practical perspective for Architects and another on stone cutting for Masons, but his approach was theoretical and difficult to understand. In his 1639 treatise he introduced many new fundamental concepts. The term 'point at infinity' (the vanishing point) appears for the first time. He also uses the ideas of a 'cone of vision' and talks about 'pencils of lines', like the lines emanating from the vanishing point, (and if you can have a point at infinity, why not more, to make lines at infinity?).
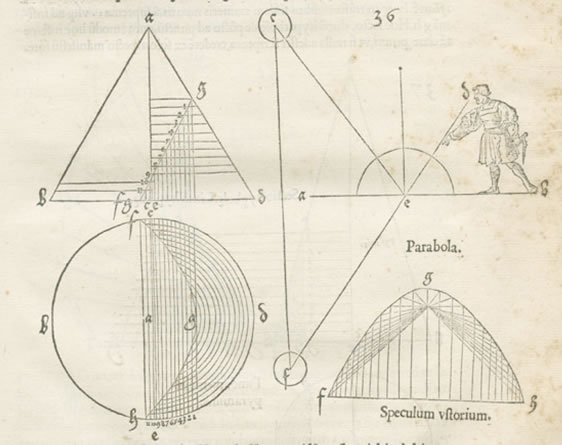
Durer's cone picture
3. Modern Geometries

Saccheri's title page
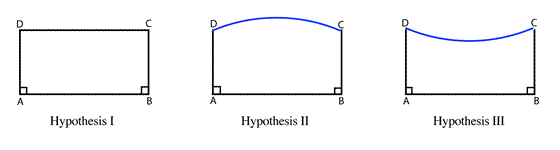
Saccheri Hypotheses Diagram

Johan Heinrich Lambert
(1728-1777)
Adrien-Marie Legendre (1752-1833) spent many years working on the parallel postulate and his efforts appear in different editions of his Éléments de géométrie. Legendre proved that the fifth postulate is equivalent to the statement that the sum of the angles of a triangle is equal to two right angles . Legendre also obtained a number of consistent but counter-intuitive results in his investigations, but was unable to bring these ideas together into a consistent system.
- In any triangle, the three angles sum to two right angles.
- In any triangle, each exterior angle equals the sum of the two internally opposite angles.
- If two parallel lines are cut by a transversal, the alternate interior angles are equal, and the corresponding angles are equal.
Carl Friedrich Gauss (1777-1855)

Carl Friedrich Gauss (1777-1855)

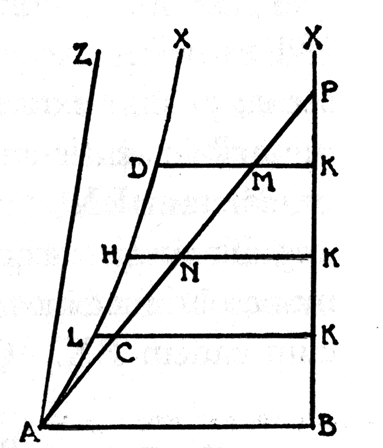
Nikolai Ivanovich Lobachevski
(1792-1856)
The red line is the boundary, the 'parallel' to the line BC.
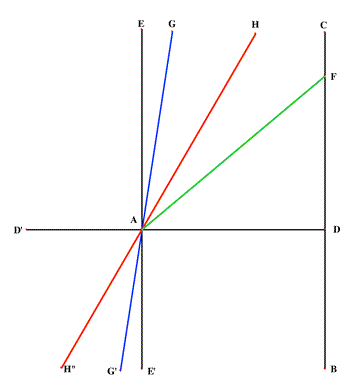
Lobachevski tried to get his work Geometrical investigations on the theory of parallels recognized, and an account in French in 1837 brought his work on non-Euclidean geometry to a wide audience but the mathematical community was not yet ready to accept these revolutionary ideas.
Lobachevski Diagram

János Bolyai (1802-1860) )
János Bolyai set out to investigate the three basic hypotheses of the right, obtuse, and acute angles by separating the case where the fifth postulate was true (the right angle case) from the cases where it was not true. On this basis he set up two systems of geometry, and searched for theorems that could be valid in both.

Eugenio Beltrami (1835-1900)
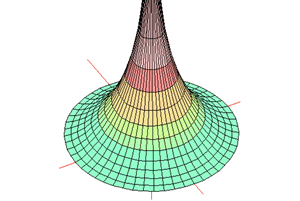
Imagine a circular polar grid (like a dart board) pulled up from the origin. It forms a trumpet-like surface. Any triangle drawn on this grid will become even more distorted when an apex is near the origin. All the lines going up the surface are asymptotes to a single central line rising vertically from the origin. These lines are all 'parallel' lines passing through a single limit point at infinity.
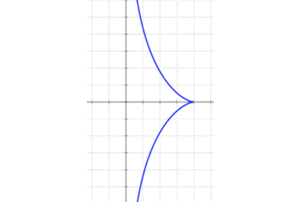
If the Tractrix is rotated about its vertical axis, the surface formed will be a complete Pseudo-sphere.
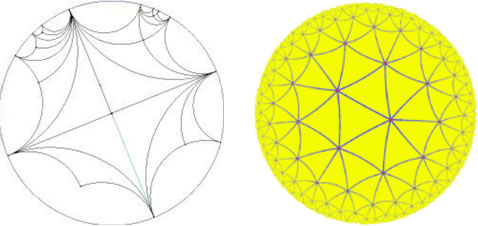
In the Poincare Model, all 'lines' are arcs of circles, except for the diameter (the arc of a circle with infinite radius). 'Parallel' lines are thought of as asymptotes where the limit point is on the circumference. With this model many 'parallels' can pass through the same point. This disc has a basic four-fold symmetry. The Yellow Poincare Disc has symmetry order seven. Maurits Escher used a
six-fold symmetry for his "Circle Limit IV" engraving - the picture with the interlocking angels and devils. For more on Escher see: http://www.mcescher.com/
For pedagogical notes: Use the notes tab at the top of this article or click here .
Notes
1. Wall quadrants were invented and used for many years by astronomers for measuring the altitude of heavenly bodies. They have been specially built as part of ancient observatories, and as they became larger had to be supported by solid walls to keep them steady. It was believed that the larger the instrument was, the more accurate were the results obtained. It is true that the larger the instrument is, the easier it is to divide the scale of the quadrant into degrees, minutes and seconds. However, the accuracy can also depend on other things like the sighting instrument. For example, telescopes were not developed well enough to be reliable until the early 18th century, and because the mounting was fixed, it had limited use. In spite of the problems, Arab astronomers were able to achieve an accuracy of about 20 seconds of arc.
Weblinks
Articles
Michele Emmer, (1993) The Visual Mind; Art and Mathematics MIT Press
J.L. Heilbron, (1998) Geometry Civilised; History, Culture and Technique . Clarendon Press, Oxford.
AND a book to look out for:
Eleanor Robson and Jackie Stedall (Editors) (December 2008), The Oxford Handbook of the History of Mathematics . Oxford University Press
You may also like
The Dangerous Ratio
This article for pupils and teachers looks at a number that even the great mathematician, Pythagoras, found terrifying.
All about Infinity
Infinity is not a number, and trying to treat it as one tends to be a pretty bad idea. At best you're likely to come away with a headache, at worse the firm belief that 1 = 0. This article discusses the different types of infinity.
Maths in the Victorian Classroom
What was it like to learn maths at school in the Victorian period? We visited the British Schools Museum in Hitchin to find out.

