Making Sixty

Age 14 to 16

Challenge Level Yellow star

Why do this problem

This problem involves a simple construction which gives a surprising and useful result. Having confirmed the sizes of angles this knowledge can be applied to make images and polyhedra. Different routes to solution can also lead to useful discussions, including how well learners explain their reasoning and the elegance of their methods.

Possible approach

Produce some equilateral triangles.

Ask the group to consider how they know they are equilateral?

Building on the idea that angles must be $60^o$, ask them to prove that this is the case.

If learners are inexperienced with proof, after lots of discussion, you may wish to use these proof cards (illustrated below) to aid in structuring a logical argument.

You may wish to give out all sixteen cards and ask learners to arrange them to form a logical argument. Alternatively, you might for example, give learners the images and ask them to write the text, or the text in order and ask them to find the pairs. The aim is to extend discussion in terms of the structure of the argument, its strengths and weaknesses or how they might have done it differently.

Learners can make triangles of different sizes by halving and quartering various sheets of paper in order to demonstrate that the paper does not have to be A4 size.

Follow on by utilising the ability to make equilateral triangles in different contexts.

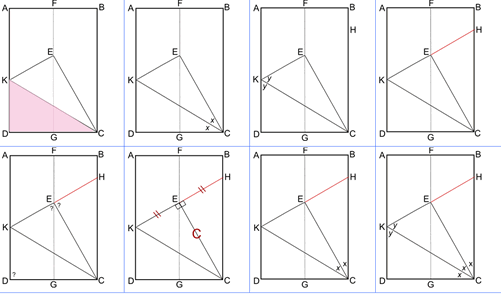
Key questions

What do you know?

Can you see and use any symmetry?

Possible support

Spending time making triangles and feeling confident about their properties is a useful starting point. Finding triangles that might be congruent, cutting them out and testing the congruency by matching them can then lead to identifying why sides and angles might be equal.

Possible extension

See:
Paper Folding - Models of the Platonic Solids.
Can learners justify all the results used as they work?

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Making Sixty

Why do this problem

Possible approach

Key questions

Possible support

Possible extension

You may also like

A Problem of Time

Quad in Quad

Arrowhead