Bochap Sudoku

Previously, I have created puzzles which used only one of the four mathematical operations ($+$, $-$, $\times$, and $\div$). In this Sudoku I have combined all the four operations together in a single puzzle. I call my new puzzle 'Bochap', which comes from a popular Hokkien word in Singapore.'Bochap' can be interpreted as 'oblivious to everything else'. Thus, the name of this new puzzle suggests that puzzlers are so focused on finding a solution that they reach a point of being 'Bochap' or oblivious of everything going on around them.

This reminds me of the story of Archimedes who, as he was drawing some diagrams on the ground, was approached by an invading Roman soldier who drew a sword over his head and asked him who he was. Too much absorbed in the diagrams on the ground, Archimedes did not give his name but, protecting the dust with his hands, exclaimed: "Don't disturb my circles!" As a result, he was slaughtered by the Roman invader!

Like the standard Sudoku, this puzzle has the basic rule:

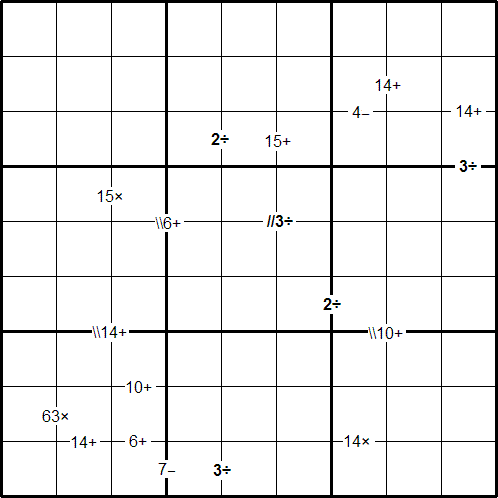
The puzzle can be solved with the help of small clue-numbers which are either placed on the border lines between selected pairs of neighbouring squares of the grid or placed after slash marks on the intersections of border lines between two diagonally adjacent squares.

Each small clue-number is the result produced in any order by a pair of digits in the two squares that are horizontally or vertically or diagonally adjacent to each other, using the mathematical operation indicated: addition ($+$), subtraction ($-$), multiplication ($\times$), and division ($\div$).

The position of each pair of diagonally adjacent squares is indicated by either two forward slash marks // or two backward slash marks \\.

For example:

The clue \\14+ on the intersection of border lines between the diagonally adjacent squares (r6c2) and (r7c3) means that possible pairs of numbers in the squares are: 7 and 7; 6 and 8, 8 and 6; 5 and 9, or 9 and 5. The clue 3$\div$ on the border line between the squares (r9c4) and (r9c5) means that possible pairs of numbers for these squares can be from the following combinations: 1 and 3, 3 and 1; 2 and 6, 6 and 2; 3 and 9, or 9 and 3.

After finding the values of all the unknown digits, the puzzle is solved by the usual sudoku technique and strategy.

 

A word document containing the Sudoku problem for classroom use, can be found here.