Can They Be Equal?
Can They be Equal? printable sheet
Charlie has been drawing rectangles:
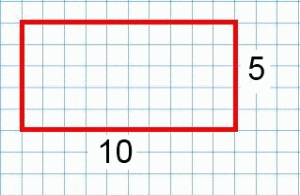
The first rectangle has a perimeter of 30 units and an area of 50 square units.
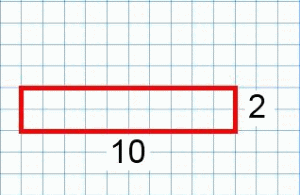
The second rectangle has a perimeter of 24 units and an area of 20 square units.
Charlie wondered if he could find a rectangle, with a side of length 10 units, whose perimeter and area have the same numerical value.
Can you find a rectangle that satisfies this condition?
Alison says "There must be lots of rectangles whose perimeter and area have the same numerical value."
Charlie is not so sure.
Can you find more examples of such rectangles?
Can you come up with a convincing argument to help Charlie and Alison decide if Alison is right?
Click here for a poster of this problem.
Related Collections
You may also like
Framed
Seven small rectangular pictures have one inch wide frames. The frames are removed and the pictures are fitted together like a jigsaw to make a rectangle of length 12 inches. Find the dimensions of the pictures.
Tilted Squares
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
Four or Five
The diagram shows a large rectangle composed of 9 smaller rectangles. If each of these rectangles has integer sides, what could the area of the large rectangle be?