Skip over navigation
Two of our best solvers, Alex from Stoke on Trent Sixth Form College and Patrick from Woodbridge School thought about this implicit equation.
$$r^2X^2-rX-r+1=0$$
Patrick looked at the first parts using the quadratic equation formula as follows:
Part 1:
If $r=1$ then $X^2-X = 0$, so $X(X-1) = 0$ and $X = 0$ or $1$.
If $r = 100$ then $100^2X^2 - 100X - 100 + 1 = 0$ so $100^2X^2-100X-99 = 0$ so
$$
X = \frac{100\pm \sqrt{100 ²+4\times 100 ²\times 99}}{ 2\times 100^2}
$$
This is real as we neither divide by $0$ nor take a negative square root.
Part 2:
If $r = 0$ then we find the equation gives $1=0$, so r cannot equal $0$.
Substituting $r^2$ for $a$, $-r$ for $b$ and $-(r-1)$ for $c$ in the usual quadratic equation formula we get
$$
X = \frac{r\pm\sqrt{r ²+4r ²(r-1)}}{2r^2}=\frac{1\pm\sqrt{1+4r-4}}{2r} = \frac{1\pm\sqrt{4r-3}}{2r}
$$
So this takes real values if and only if $4r - 3 \geq 0$.
Alex realised that the key feature of this problem was the discriminant of the quadratic equations in $X$, and looked at that object directly:
The discriminant determines whether a quadratic has real roots, therefore $X(r)$ will have real values if and only if the discriminant $D$ of the quadratic is zero or positive.
$$
\begin{eqnarray}
D&\geq 0&\cr
\Rightarrow (-r)^2 - 4(r^2)(1-r) &\geq& 0 \cr
\Rightarrow r^2 - 4r^2 + 4r^3 &\geq& 0\cr
\Rightarrow 4r^3 &\geq& 3r^2\cr
\Rightarrow r &\geq& 3/4
\end{eqnarray}
$$
So, $X(r)$ has real values for $r\geq 3/4$.
This means that $X(1)$ and $X(100)$ have real values, but $X(-1)$ does not. $X(0)$ is undefined because the corresponding equation $(1=0)$ has no solutions, it is a contradiction.
Alex also correctly deduced the maximum and minimum values of $X(r)$
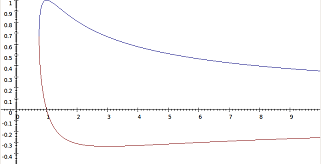
The maximum value of $X(r)$ is $X(1) = 1$. The minimum value of $X(r)$ is $X(3) = -1/3$. The graph has an asymptote $r = 0$.
Alex submitted a plot of the associated curve, which shows two distinct branches.
Steve solved this problem in the following way:
$$X = \frac{-b \pm \sqrt{b^2 - 4ac}} {2a}$$
$$X = \frac {1 \pm \sqrt{4r - 3}}{2r}$$
$X$ is therefore real for all $r$ greater than or equal to $\frac{3}{4}$
Hence $r = 0$ and $-1$ give complex roots of $X$ but $1$ and $100$ give real roots.
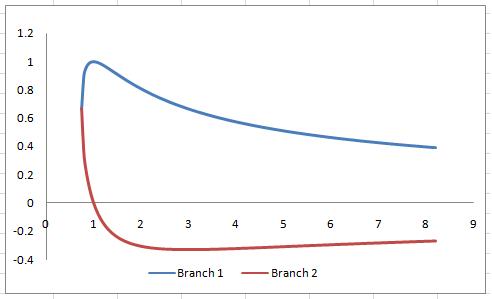
Asymptote at $r = 0$
As $r \to \infty$, $X \to 0$
$$\frac{\mathrm{d}X}{\mathrm{d}r} = \frac{\mathrm{d}}{\mathrm{d}r} \left[ \frac{1}{2r} \left(1 \pm \sqrt{4r - 3} \right) \right] = \frac{-2 \left( \sqrt{4r-3} \right) +4r-6} {r^2 \sqrt{4r-3}}$$
Setting $\displaystyle \frac{\mathrm{d}X}{\mathrm{d}r} = 0$ we find $r = 1,\ 3$
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Implicitly
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Two of our best solvers, Alex from Stoke on Trent Sixth Form College and Patrick from Woodbridge School thought about this implicit equation.
$$r^2X^2-rX-r+1=0$$
Patrick looked at the first parts using the quadratic equation formula as follows:
Part 1:
If $r=1$ then $X^2-X = 0$, so $X(X-1) = 0$ and $X = 0$ or $1$.
If $r = 100$ then $100^2X^2 - 100X - 100 + 1 = 0$ so $100^2X^2-100X-99 = 0$ so
$$
X = \frac{100\pm \sqrt{100 ²+4\times 100 ²\times 99}}{ 2\times 100^2}
$$
This is real as we neither divide by $0$ nor take a negative square root.
Part 2:
If $r = 0$ then we find the equation gives $1=0$, so r cannot equal $0$.
Substituting $r^2$ for $a$, $-r$ for $b$ and $-(r-1)$ for $c$ in the usual quadratic equation formula we get
$$
X = \frac{r\pm\sqrt{r ²+4r ²(r-1)}}{2r^2}=\frac{1\pm\sqrt{1+4r-4}}{2r} = \frac{1\pm\sqrt{4r-3}}{2r}
$$
So this takes real values if and only if $4r - 3 \geq 0$.
Alex realised that the key feature of this problem was the discriminant of the quadratic equations in $X$, and looked at that object directly:
The discriminant determines whether a quadratic has real roots, therefore $X(r)$ will have real values if and only if the discriminant $D$ of the quadratic is zero or positive.
$$
\begin{eqnarray}
D&\geq 0&\cr
\Rightarrow (-r)^2 - 4(r^2)(1-r) &\geq& 0 \cr
\Rightarrow r^2 - 4r^2 + 4r^3 &\geq& 0\cr
\Rightarrow 4r^3 &\geq& 3r^2\cr
\Rightarrow r &\geq& 3/4
\end{eqnarray}
$$
So, $X(r)$ has real values for $r\geq 3/4$.
This means that $X(1)$ and $X(100)$ have real values, but $X(-1)$ does not. $X(0)$ is undefined because the corresponding equation $(1=0)$ has no solutions, it is a contradiction.
Alex also correctly deduced the maximum and minimum values of $X(r)$
The maximum value of $X(r)$ is $X(1) = 1$. The minimum value of $X(r)$ is $X(3) = -1/3$. The graph has an asymptote $r = 0$.
Alex submitted a plot of the associated curve, which shows two distinct branches.

Steve solved this problem in the following way:
Part 1:
$$X = \frac{-b \pm \sqrt{b^2 - 4ac}} {2a}$$
$$X = \frac {1 \pm \sqrt{4r - 3}}{2r}$$
$X$ is therefore real for all $r$ greater than or equal to $\frac{3}{4}$
Hence $r = 0$ and $-1$ give complex roots of $X$ but $1$ and $100$ give real roots.
Part 2:

Asymptote at $r = 0$
As $r \to \infty$, $X \to 0$
Part 3:
$$\frac{\mathrm{d}X}{\mathrm{d}r} = \frac{\mathrm{d}}{\mathrm{d}r} \left[ \frac{1}{2r} \left(1 \pm \sqrt{4r - 3} \right) \right] = \frac{-2 \left( \sqrt{4r-3} \right) +4r-6} {r^2 \sqrt{4r-3}}$$
Setting $\displaystyle \frac{\mathrm{d}X}{\mathrm{d}r} = 0$ we find $r = 1,\ 3$

