Skip over navigation
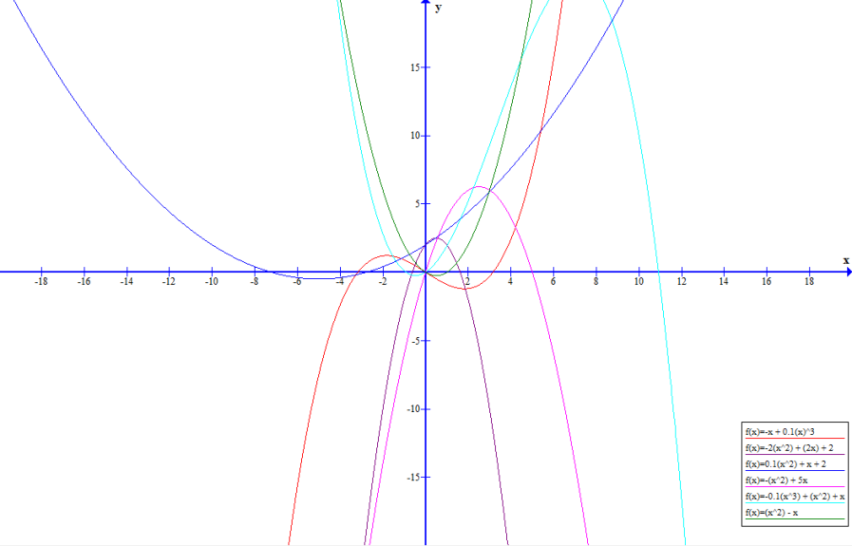
The graph above shows a plot of each of the forms of the given reactions around the origin. More complex behaviour is seen once the scale is expanded due to the relative dominance of constants, t, t$^2$ and t$^3$ terms at different points on the x- axis. In the graph above x is equivalent to t.
Describing each of the trends in words is useful to consider how each reaction progresses in relation to the algebraic form given. Intercepts and key points can often be found by equating R$_n$ to 0. Turning points can be found by differentiating the form of the rate of reaction and solving.
R$_1$: The reaction does not start for a period of 10$^{\frac{1}{2}}$ time units. After this point however the rate of reaction increases with time due to the dominance of the t$^3$ at large values of t.
R$_2$: The reaction starts immediately due to the constant in the equation for the rate. However, it rapidly reaches a peak rate at t= 0.5 units due to a pattern of behaviour that can be seen as a shift between the linear 2t term being dominant to the -2t$^2$ having greater influence. After this beak the rate of reaction rapidly falls and comes to a stop after 1.62 time units.
R$_3$: The reaction starts immediately and the rate of reaction continues to speed up over times due to the fact that both the t and 0.1t$^2$ terms are both positive meaning that there is a transition to an overall t$^2$ type behaviour for the rate of reaction, as t grows large.
R$_4$: The 5t term means that the form of the rate curve shows a very rapid increase in rate of reaction initially. The increase in the rate of the reaction drops off from the initial rate until it reaches a peak at 2.5 time units. There is symmetrical behaviour as the rate of reaction decreases increasingly rapidly until the reaction comes to a stop at 5 units.
R$_5$: The rate of reaction increases rapidly due to the initial dominance of the t and t$^2$ terms. Rate of reaction peaks at around 7 time units after which there is a very rapid decrease due to the influence of the negative -0.1t$^3$. The reaction comes to a stop after 10.9 time units.
R$_6$: The rate of reaction is initially 0 for a period of 1 time units after which there is a rapid rate of increase due to the t$^2$ term counteracting the -t term and dominating the form the equationat large values of t.
After considering how the rate of reaction varies over time, the rest of the questions are elementary.
R$_2$ and R$_3$ react immediately due to the presence of constants in their algebraic forms.
R$_1$ and R$_6$ take a while to get started due to the negative t terms within their algebraic terms which are dominant at smaller values of t.
R$_1$, R$_3$ and R$_6$ have a continually increasing rate of reaction as t becomes large and $\text{t} \rightarrow +\infty$ due to the presence of t$^2$ and t$^3$ terms which are dominant at large values of t.
R$_2$, R$_4$ and R$_5$ speed up to a peak and then slow down due to a transition in the dominant term in the algebraic form as t gets larger.
In the case of R$_4$, the initial dominance of the 5t term is then replaced by a -t$^2$ term which causes a peak at t = 2.5 a then a slowing of the reaction as the -t$^2$ gives an increasingly negative contribution as t increases. R$_2$ shows a similar relationship but the smaller coefficient of the t term means that the peak occurs far sooner i.e. at smaller t.
For R$_5$, a similar transition between a dominant positive t$^2$ to a dominant negative -0.1t$^3$ at t large enough to overcome the coefficient of the cubed term, causes the rate of reaction to all dramatically after peaking.
R$_2$, R$_4$ and R$_5$ are also the reactions that eventually stop due to the dominant term at large t being a negative term causing a rapid slowing of the rate of reaction.
It is clear that R$_1$ would take longest to get started if you consider the form of its algebraic equation compared with R$_6$.
R$_1$(t) = -t + 0.1t$^3$
R$_6$(t) = -t + t$^2$
At low values of t both expressions have a dominant -t term. However for R$_1$ the fact that the term has a coefficient of 0.1 means that it takes far larger values of t for this t$^3$ term to become dominant and counteract the contribution of the -t term. The t$^2$ term in R$_6$ does not have a coefficient thus the reaction is able to start after t=1.
R$_1$ is also the reaction which will be the fastest after a long period of time. This is because of the value of the t$^3$ term rises faster than any other terms present as the dominant term at large t for all other reactions. The coefficient of 0.1 is easily overcome at large t.
The plot above demonstrates which reactions will be the fastest close to the origin and expansion of the scale will aid consideration of the fastest reaction at higher values of t. A graphical solution is not at all essential. An appreciation of the dominant terms in an equation at differenent values of t is more important. It is revealed that all of the reactions are, at some point, the fastest reaction!
R$_2 \rightarrow$ R$_3 \rightarrow$ R$_4 \rightarrow$ R$_5 \rightarrow$ R$_6 \rightarrow$ R$_1$
As identified previously, R$_2$ and R$_3$ are reactions that start immediately. The fact that R$_2$ has a coefficient of 2 in front of its t term is enough to mean that it is the fastest reaction initially. However, we also know that R$_2$ is a reaction that has a peak rate, slows down and eventually stops. This means that R$_3$ which has a continuously increasing rate, is the fastest reaction for a brief period. The time at which this occurs can be calculated:
2 + 2t - 2t$^2$ = 2 + t + 0.1t$^2$
2.1t^2 - t = 0
t = $\frac{1 \pm \sqrt{1}}{2(2.1)}$
where the required solution is t = 0.47 (2dp)
R$_3$ is only the fastest reaction for a small period of time as at small t, the t$^2$ term is not as large as the 5t component of R$^4$. It is known that R$^4$ has a rapid initial rise in the rate of reaction due to this term. The point of intersection can again be calculated:
5t - t$^2$ = 2 + t + 0.1t$^2$
1.1t$^2$ -4t + 2 = 0
t = $\frac{4 \pm \sqrt{6 - 4(2)(1.1)}}{2(1.1)}$
where the required solution is t = 0.60 (2dp)
It is also known that R$^4$ has a curve that peaks at t=2.5 and falls off, eventually stopping so it cannot be the fastest reaction for a long period of time. The next most likely candidate is R$_5$ as when the t$^2$ term becomes dominant causing R$^4$ to peak and fall, the positive t$^2$ for R$_5$ will become influential, particularly considering that R$_5$ also has a positive t term meaning a good initial rise in reaction rate. The point of intersection between R$^4$ and R$_5$ in the required region can be calculated.
-t$^2$ + 5t = -0.1t$^3$ + t$^2$ + t
0.1t$^3$ - 2t$^2$ + 4t = 0
t(0.1t$^2$ - 2t + 4) = 0
t = $\frac{2 \pm \sqrt{4 - 4(4)(0.1)}}{2(0.1)}$
where the required solution is t = 2.25 (2dp)
However, as R$_5$ has a negative -0.1t$^3$ term its is known to peak and then slow down, eventually stopping. An equation that has a positive t$^2$ is a likely candidate for the fastest reaction at this point considering that the t$^3$ in all the reactions given have low coefficients. R$_6$ is the reaction that fits this criterion and is known to be a reaction where the rate keeps on speeding up.The point of intersection with R$_5$ is given by:
-0.1t$^3$ + t$^2$ + t = t$^2$ - t
-0.1t$^3$ + 2t = 0
t(-0.1t$^2$ + 2) = 0
t = $\frac{\pm \sqrt{- 4(2)(-0.1)}}{2(-0.1)}$
where the required solution is t = 4.47 (2dp)
We already know that R$_1$ is the fastest reaction in the long term due to the t$^3$ term. The point of intersection with the R$_6$ in this region can again be found:
t$^2$ - t = -t + 0.1t$^3$
0.1t$^3$ - t$^2$ = 0
t$^2$(0.1t - 1) = 0
where the required solution is t = 10
Thus we have managed to calculate the times over which each of these reactions is the fastest.
R$_2$ for 0 < t < 0.47
R$_3$ for 0.47 < t < 0.60
R$_4$ for 0.60 < t < 2.25
R$_5$ for 2.25 < t < 4.47
R$_6$ for 4.47 < t < 10
R$_1$ for t > 10

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Reaction Types
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources

The graph above shows a plot of each of the forms of the given reactions around the origin. More complex behaviour is seen once the scale is expanded due to the relative dominance of constants, t, t$^2$ and t$^3$ terms at different points on the x- axis. In the graph above x is equivalent to t.
Describing each of the trends in words is useful to consider how each reaction progresses in relation to the algebraic form given. Intercepts and key points can often be found by equating R$_n$ to 0. Turning points can be found by differentiating the form of the rate of reaction and solving.
R$_1$: The reaction does not start for a period of 10$^{\frac{1}{2}}$ time units. After this point however the rate of reaction increases with time due to the dominance of the t$^3$ at large values of t.
R$_2$: The reaction starts immediately due to the constant in the equation for the rate. However, it rapidly reaches a peak rate at t= 0.5 units due to a pattern of behaviour that can be seen as a shift between the linear 2t term being dominant to the -2t$^2$ having greater influence. After this beak the rate of reaction rapidly falls and comes to a stop after 1.62 time units.
R$_3$: The reaction starts immediately and the rate of reaction continues to speed up over times due to the fact that both the t and 0.1t$^2$ terms are both positive meaning that there is a transition to an overall t$^2$ type behaviour for the rate of reaction, as t grows large.
R$_4$: The 5t term means that the form of the rate curve shows a very rapid increase in rate of reaction initially. The increase in the rate of the reaction drops off from the initial rate until it reaches a peak at 2.5 time units. There is symmetrical behaviour as the rate of reaction decreases increasingly rapidly until the reaction comes to a stop at 5 units.
R$_5$: The rate of reaction increases rapidly due to the initial dominance of the t and t$^2$ terms. Rate of reaction peaks at around 7 time units after which there is a very rapid decrease due to the influence of the negative -0.1t$^3$. The reaction comes to a stop after 10.9 time units.
R$_6$: The rate of reaction is initially 0 for a period of 1 time units after which there is a rapid rate of increase due to the t$^2$ term counteracting the -t term and dominating the form the equationat large values of t.
After considering how the rate of reaction varies over time, the rest of the questions are elementary.
R$_2$ and R$_3$ react immediately due to the presence of constants in their algebraic forms.
R$_1$ and R$_6$ take a while to get started due to the negative t terms within their algebraic terms which are dominant at smaller values of t.
R$_1$, R$_3$ and R$_6$ have a continually increasing rate of reaction as t becomes large and $\text{t} \rightarrow +\infty$ due to the presence of t$^2$ and t$^3$ terms which are dominant at large values of t.
R$_2$, R$_4$ and R$_5$ speed up to a peak and then slow down due to a transition in the dominant term in the algebraic form as t gets larger.
In the case of R$_4$, the initial dominance of the 5t term is then replaced by a -t$^2$ term which causes a peak at t = 2.5 a then a slowing of the reaction as the -t$^2$ gives an increasingly negative contribution as t increases. R$_2$ shows a similar relationship but the smaller coefficient of the t term means that the peak occurs far sooner i.e. at smaller t.
For R$_5$, a similar transition between a dominant positive t$^2$ to a dominant negative -0.1t$^3$ at t large enough to overcome the coefficient of the cubed term, causes the rate of reaction to all dramatically after peaking.
R$_2$, R$_4$ and R$_5$ are also the reactions that eventually stop due to the dominant term at large t being a negative term causing a rapid slowing of the rate of reaction.
It is clear that R$_1$ would take longest to get started if you consider the form of its algebraic equation compared with R$_6$.
R$_1$(t) = -t + 0.1t$^3$
R$_6$(t) = -t + t$^2$
At low values of t both expressions have a dominant -t term. However for R$_1$ the fact that the term has a coefficient of 0.1 means that it takes far larger values of t for this t$^3$ term to become dominant and counteract the contribution of the -t term. The t$^2$ term in R$_6$ does not have a coefficient thus the reaction is able to start after t=1.
R$_1$ is also the reaction which will be the fastest after a long period of time. This is because of the value of the t$^3$ term rises faster than any other terms present as the dominant term at large t for all other reactions. The coefficient of 0.1 is easily overcome at large t.
The plot above demonstrates which reactions will be the fastest close to the origin and expansion of the scale will aid consideration of the fastest reaction at higher values of t. A graphical solution is not at all essential. An appreciation of the dominant terms in an equation at differenent values of t is more important. It is revealed that all of the reactions are, at some point, the fastest reaction!
R$_2 \rightarrow$ R$_3 \rightarrow$ R$_4 \rightarrow$ R$_5 \rightarrow$ R$_6 \rightarrow$ R$_1$
As identified previously, R$_2$ and R$_3$ are reactions that start immediately. The fact that R$_2$ has a coefficient of 2 in front of its t term is enough to mean that it is the fastest reaction initially. However, we also know that R$_2$ is a reaction that has a peak rate, slows down and eventually stops. This means that R$_3$ which has a continuously increasing rate, is the fastest reaction for a brief period. The time at which this occurs can be calculated:
2 + 2t - 2t$^2$ = 2 + t + 0.1t$^2$
2.1t^2 - t = 0
t = $\frac{1 \pm \sqrt{1}}{2(2.1)}$
where the required solution is t = 0.47 (2dp)
R$_3$ is only the fastest reaction for a small period of time as at small t, the t$^2$ term is not as large as the 5t component of R$^4$. It is known that R$^4$ has a rapid initial rise in the rate of reaction due to this term. The point of intersection can again be calculated:
5t - t$^2$ = 2 + t + 0.1t$^2$
1.1t$^2$ -4t + 2 = 0
t = $\frac{4 \pm \sqrt{6 - 4(2)(1.1)}}{2(1.1)}$
where the required solution is t = 0.60 (2dp)
It is also known that R$^4$ has a curve that peaks at t=2.5 and falls off, eventually stopping so it cannot be the fastest reaction for a long period of time. The next most likely candidate is R$_5$ as when the t$^2$ term becomes dominant causing R$^4$ to peak and fall, the positive t$^2$ for R$_5$ will become influential, particularly considering that R$_5$ also has a positive t term meaning a good initial rise in reaction rate. The point of intersection between R$^4$ and R$_5$ in the required region can be calculated.
-t$^2$ + 5t = -0.1t$^3$ + t$^2$ + t
0.1t$^3$ - 2t$^2$ + 4t = 0
t(0.1t$^2$ - 2t + 4) = 0
t = $\frac{2 \pm \sqrt{4 - 4(4)(0.1)}}{2(0.1)}$
where the required solution is t = 2.25 (2dp)
However, as R$_5$ has a negative -0.1t$^3$ term its is known to peak and then slow down, eventually stopping. An equation that has a positive t$^2$ is a likely candidate for the fastest reaction at this point considering that the t$^3$ in all the reactions given have low coefficients. R$_6$ is the reaction that fits this criterion and is known to be a reaction where the rate keeps on speeding up.The point of intersection with R$_5$ is given by:
-0.1t$^3$ + t$^2$ + t = t$^2$ - t
-0.1t$^3$ + 2t = 0
t(-0.1t$^2$ + 2) = 0
t = $\frac{\pm \sqrt{- 4(2)(-0.1)}}{2(-0.1)}$
where the required solution is t = 4.47 (2dp)
We already know that R$_1$ is the fastest reaction in the long term due to the t$^3$ term. The point of intersection with the R$_6$ in this region can again be found:
t$^2$ - t = -t + 0.1t$^3$
0.1t$^3$ - t$^2$ = 0
t$^2$(0.1t - 1) = 0
where the required solution is t = 10
Thus we have managed to calculate the times over which each of these reactions is the fastest.
R$_2$ for 0 < t < 0.47
R$_3$ for 0.47 < t < 0.60
R$_4$ for 0.60 < t < 2.25
R$_5$ for 2.25 < t < 4.47
R$_6$ for 4.47 < t < 10
R$_1$ for t > 10
You may also like
Power Up
Show without recourse to any calculating aid that 7^{1/2} + 7^{1/3} + 7^{1/4} < 7 and 4^{1/2} + 4^{1/3} + 4^{1/4} > 4 . Sketch the graph of f(x) = x^{1/2} + x^{1/3} + x^{1/4} -x

