At Right Angles
At Right Angles printable sheet
This problem follows on from How Steep is the Slope?
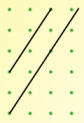
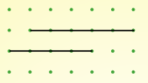
It's easy to draw parallel lines - just check that the gradients match.
 |
 |
 |
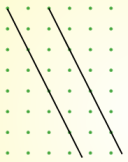| Gradient $\frac{3}{2}$ | Gradient $0$ | Gradient $-2$ |
But I'm finding it harder to draw perpendicular lines. Here are my best efforts so far but I don't think they're quite right!
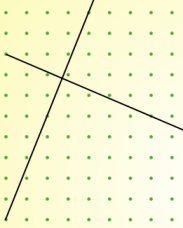
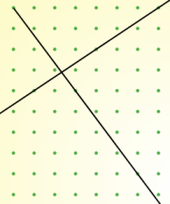
I know that the sides of a square are at right angles, so if I learn to draw tilted squares I may be able to find an efficient method for drawing perpendicular lines.
Experiment with the interactivity below until you can draw squares with confidence.
Work out the gradients of the lines which form your squares.
Is there a relationship between the gradients of perpendicular lines?
Can you use your relationship to explain why the two sets of lines above are not perpendicular?
Full Screen Version
| First line | Second line | ||||||||
| Through (6,9) and (10,1) | Through (4,2) and (14,7) | ||||||||
| Through (6,8) and (21,12) | Through (1,4) and (5,14) | ||||||||
| Through (-3,-2) and (-1,1) | Through (6,1) and (15,-5) |
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Doesn't Add Up
In this problem we are faced with an apparently easy area problem, but it has gone horribly wrong! What happened?
From All Corners
Straight lines are drawn from each corner of a square to the mid points of the opposite sides. Express the area of the octagon that is formed at the centre as a fraction of the area of the square.