Reflecting Lines
Reflecting Lines printable sheet
Here are two sets of graphs. Each shows a pair of lines which are reflections of each other, one in the horizontal axis and one in the vertical axis.
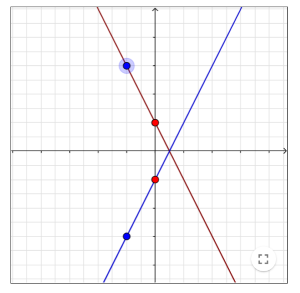
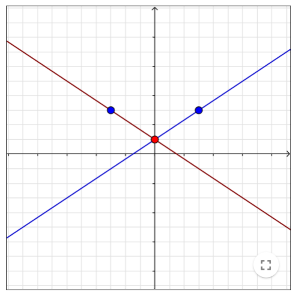
Move the red and blue dots on the interactivity below to create some more pairs of reflected lines.
What can you say about the equations of two lines if one is a reflection of the other in the horizontal axis? What about a reflection in the vertical axis?
|
$y=3x+\frac14$ |
$y=4x+3$ | $y=2x+4$ | $y=2x+\frac14$ |
$y=-\frac14x+3$ |
$y=-4x-2$ | $y=\frac14x+2$ | $y=-2x-4$ |
$y=-\frac14x+2$ |
$y=3x+4$ | $y=-3x-\frac14$ | $y=\frac14x-3$ |
$y=-2x+\frac14$ |
$y=-4x+3$ | $y=4x+2$ | $y=-3x+4$ |
Now imagine that a line is reflected in one of the axes and the image is then reflected in the other.
Can you predict the equation of the resulting line if you know the equation of the original?
Does it make a difference which axis you choose to reflect in first?
Explain your findings.
Related Collections
You may also like
Frieze Patterns in Cast Iron
A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.
The Frieze Tree
Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?
Friezes
Some local pupils lost a geometric opportunity recently as they surveyed the cars in the car park. Did you know that car tyres, and the wheels that they on, are a rich source of geometry?