Gravity Paths

• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

An object of mass $m$, perhaps a spaceman, is dropped from rest in space and accelerates under the influence of a series of stationary planets.

In each of the following seven scenarios, the red planets have the same mass $M$ and lie with their centres on grid axes. Assume that all of the masses are in a plane, so that the motion is entirely two-dimensional.

For the indicated placement of the object (black circle), in which cases can you describe for certain the subsequent qualitative form of the motion? In which cases are there a variety of possible motion types, depending on the magnitudes of $m$ and $M$? Where the form of the motion is unclear, you might be able to use Newton's law of gravitation to help resolve the uncertainties.



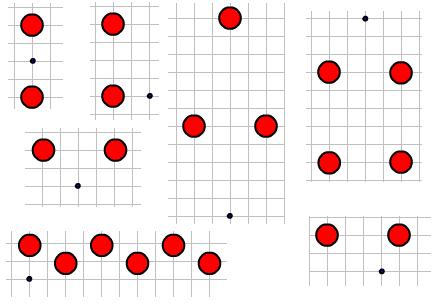
Use vectors to determine in each case the exact direction in which the object will start to fall.

Discussion: in each diagram, can you locate a set of initial points for which the object would never fall into one of the planets? Can you be sure that you have found all such points?