Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Right Volume
Age 16 to 18
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
If we suppose that the curve $y=f(x)$ is integrable then the volume created will be
$$
V = \int^1_0 \pi y^2 dx\;.
$$
To get a feel for the sort of curve we might need, first consider the special case $y=x$, which clearly passes through the two points. Then,
$$
V = \int^1_0 \pi x^2 = \pi\left[\frac{x^3}{3}\right]^1_0 = \frac{\pi}{3}\;.
$$
This is slightly larger than $1$, so we could consider a family of curves which are beneath $y=x$.
We could look for a curve like the blue one in the diagram below:
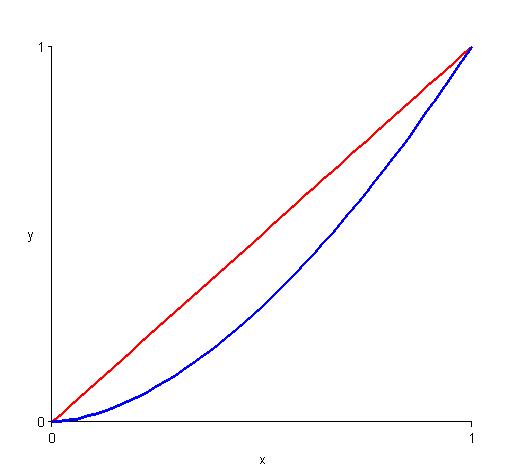
This looks like a section of a polynomial which has a root at $0$.
How about $y=x^4$?
Then,
$$
V = \int^1_0 \pi x^8 = \pi\left[\frac{x^9}{9}\right]^1_0 = \frac{\pi}{9}\;.
$$
This is still not right, but I think a polynomial could work.
Let's try $y=x^a$ where $a$ is a real number.
Then,
$$
V = \int^1_0 \pi x^{2a} = \pi\left[\frac{x^{2a+1}}{2a+1}\right]^1_0 = \frac{\pi}{2a+1}\;.
$$
If we let $a=(\pi-1)/2$ then the volume is $1$.
Therefore a solution is$$
There are, of course, others!
$$
V = \int^1_0 \pi y^2 dx\;.
$$
To get a feel for the sort of curve we might need, first consider the special case $y=x$, which clearly passes through the two points. Then,
$$
V = \int^1_0 \pi x^2 = \pi\left[\frac{x^3}{3}\right]^1_0 = \frac{\pi}{3}\;.
$$
This is slightly larger than $1$, so we could consider a family of curves which are beneath $y=x$.
We could look for a curve like the blue one in the diagram below:

This looks like a section of a polynomial which has a root at $0$.
How about $y=x^4$?
Then,
$$
V = \int^1_0 \pi x^8 = \pi\left[\frac{x^9}{9}\right]^1_0 = \frac{\pi}{9}\;.
$$
This is still not right, but I think a polynomial could work.
Let's try $y=x^a$ where $a$ is a real number.
Then,
$$
V = \int^1_0 \pi x^{2a} = \pi\left[\frac{x^{2a+1}}{2a+1}\right]^1_0 = \frac{\pi}{2a+1}\;.
$$
If we let $a=(\pi-1)/2$ then the volume is $1$.
Therefore a solution is
$$
y=x^{(\pi-1)/2}\;.
$$
There are, of course, others!
You may also like
A Close Match
Can you massage the parameters of these curves to make them match as closely as possible?

