Skip over navigation
You've maybe come across a challenge of putting five squares together in different ways - often called pentominoes.
So here are five squares and four ways of putting them together - there are obviously more ways. (You could try the Penta Place problem if you haven't seen this before.)
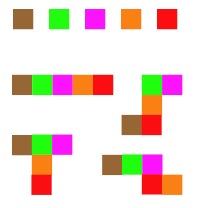
Please send in all the different shapes you can get and let us know how you made sure you had found them all.
Perhaps you also have some ideas about how you may go further with the question "I wonder what would happen if I ...?"
Hexpentas
Age 5 to 11
Challenge Level 
You've maybe come across a challenge of putting five squares together in different ways - often called pentominoes.
So here are five squares and four ways of putting them together - there are obviously more ways. (You could try the Penta Place problem if you haven't seen this before.)
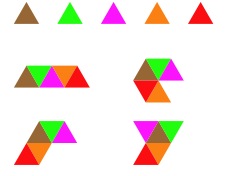
You may even have done a similar
challenge using triangles (if not have a go at our
Tri-five problem). Like this:
But the challenge for today is to consider the same idea using
hexagons.
So, the challenge is:
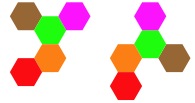
What different shapes can you make using five hexagons?
Be careful that you do not have any the same as each other.
For example, these two look different but are in fact
identical:
Please send in all the different shapes you can get and let us know how you made sure you had found them all.
Perhaps you also have some ideas about how you may go further with the question "I wonder what would happen if I ...?"
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
