Skip over navigation
So, for example, I found that the first cube, $3$ by $3$ by $3$, used $27$ cubes.
The same cube with holes used $20$ cubes, a difference of $7$.
How about exploring the numbers for the next few Solid and Frame cubes?
Holes
Age 5 to 11
Challenge Level 
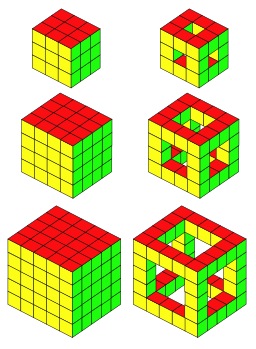
Here we have three solid cubes and three cubes that have holes.
They're just the first three in a series that could go on and on.I was wondering about the number of cubes used in each ...
Then I thought about the difference between those numbers.
So, for example, I found that the first cube, $3$ by $3$ by $3$, used $27$ cubes.
The same cube with holes used $20$ cubes, a difference of $7$.
You can call these types of cubes what you like but I called them "Solid" and "Frame".
How about exploring the numbers for the next few Solid and Frame cubes?
Do you notice any patterns?
Can you explain any of the patterns?
You may also like
Cereal Packets
How can you put five cereal packets together to make different shapes if you must put them face-to-face?