Sticky Numbers

Why do this problem?

This problem requires some knowledge of square numbers, but more importantly requires students to think strategically and provide convincing arguments and justifications for their findings

Possible approach

Introduce the problem using the example $10, 15, 21, 4, 5$, explaining that this list of numbers is special because each pair of adjacent numbers add up to make a square number.

Set them the challenge to produce a similar list using all the numbers from $1$ to $17$. Hand out sets of these cards and ask students to work in pairs on this challenge.

After the class have had a few minutes to work on this, add that you would like to know all the possible different ways of making such a list. Challenge them to produce a convincing argument that they have found all the possibilities.

Finally, ask students to present their solutions and justifications to the rest of the class.

An alternative starting point for this lesson could be to ask for 17 volunteers to stand at the front holding one of these cards. With help from the rest of the class, ask them to arrange themselves to satisfy the criteria above. Once they have found a solution, ask them to work in pairs as outlined above to find all the possible arrangements and justify that they have the complete set.

Key questions

Possible support

Students could make a table listing the numbers which can be paired with each of the numbers from $1$ to $17$ to make a square total.

Possible extension

This graph has the numbers from $1$ to $31$ at its vertices. Each edge connects two numbers which add together to make a square number.

Can you use the graph to produce a list of all the numbers from $1$ to $31$ so that pairs of adjacent numbers add up to a square number? Is there more than one way to do it?



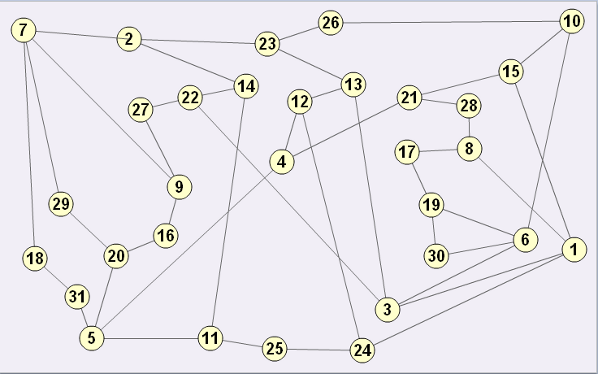
Can you find any other numbers $n$ less than $31$ so that all the numbers from $1$ to $n$ can be written in a list in this way? How does the graph help you? Here is a printable version of the graph.