Dicey Operations
This game follows on from Nice or Nasty. You might like to try Dicey Addition before playing this game.
Again, there are several games to choose from.
Find a partner and a 1-6 dice, or preferably a 0-9 dice if you have one. The interactivity in Dice and Spinners can be used to simulate throwing different dice.
Take turns to throw the dice and decide which of your cells to fill.
This can be done in two ways: either fill in each cell as you throw the dice, or collect all your numbers and then decide where to place them.
Game 1
Each of you draw an addition grid like this:
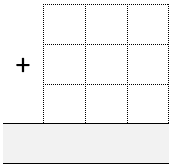
Throw the dice nine times each until all the cells are full.
Whoever has the sum closest to 1000 wins.
There are two possible scoring systems:
- A point for a win. The first person to reach 10 wins the game.
- Each player keeps a running total of their "penalty points", the difference between their result and 1000 after each round. First to 5000 loses.
You can vary the target to make it easier or more difficult.
Game 2
Each of you draw a subtraction grid like this:
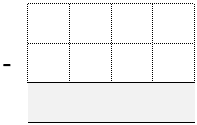
Throw the dice eight times each until all the cells are full.
Whoever has the difference closest to 1000 wins.
There are two possible scoring systems:
- A point for a win. The first person to reach 10 wins the game.
- Each player keeps a running total of their "penalty points", the difference between their result and 1000 after each round. First to 5000 loses.
Game 3
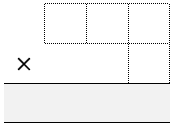
Whoever has the product closest to 1000 wins.
There are two possible scoring systems:
- A point for a win. The first person to reach 10 wins the game.
- Each player keeps a running total of their "penalty points", the difference between their result and 1000 after each round. First to 5000 loses.
Game 4
Each of you draw a multiplication grid like this:
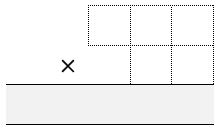
Throw the dice five times each until all the cells are full.
Whoever has the product closest to 10000 wins.
- A point for a win. The first person to reach 10 wins the game.
- Each player keeps a running total of their "penalty points", the difference between their result and 10000 after each round. First to 10000 loses.
Game 5
Whoever has the answer closest to 1000 wins.
There are two possible scoring systems:
- A point for a win. The first person to reach 10 wins the game.
- Each player keeps a running total of their "penalty points", the difference between their result and 1000 after each round. First to 5000 loses.
Game 6
Each of you draw a division grid like this:
Throw the dice six times each until all the cells are full.
Whoever has the answer closest to 100 wins.
There are two possible scoring systems:
- A point for a win. The first person to reach 10 wins the game.
- Each player keeps a running total of their "penalty points", the difference between their result and 100 after each round. First to 500 loses.
You can vary the target to make it easier or more difficult.
You may like to make use of this Operation Grid/Scoring Sheet
You may also like
Greetings
From a group of any 4 students in a class of 30, each has exchanged Christmas cards with the other three. Show that some students have exchanged cards with all the other students in the class. How many such students are there?
Writ Large
Suppose you had to begin the never ending task of writing out the natural numbers: 1, 2, 3, 4, 5.... and so on. What would be the 1000th digit you would write down.
Euromaths
How many ways can you write the word EUROMATHS by starting at the top left hand corner and taking the next letter by stepping one step down or one step to the right in a 5x5 array?