Stereoisomers

• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

Stereoisomers are isomeric molecules that have the same molecular formula and sequence of bonded atoms, but which differ ONLY in the three-dimensional orientation of their atoms in space.

Look below at the three pairs of molecules. In each case, can the molecule on the left be rotated in any way such that it can be superimposed onto the molecule on the right?


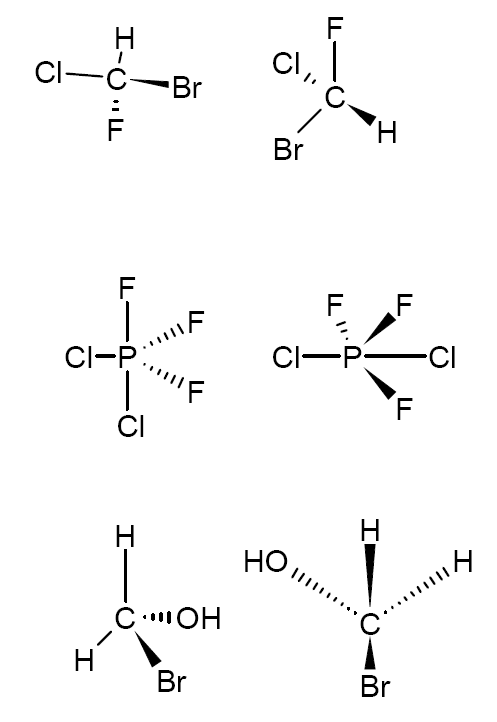
Enantiomers are two stereoisomers that are related to each other by reflection: they are mirror images of each other which are non-superimposable.

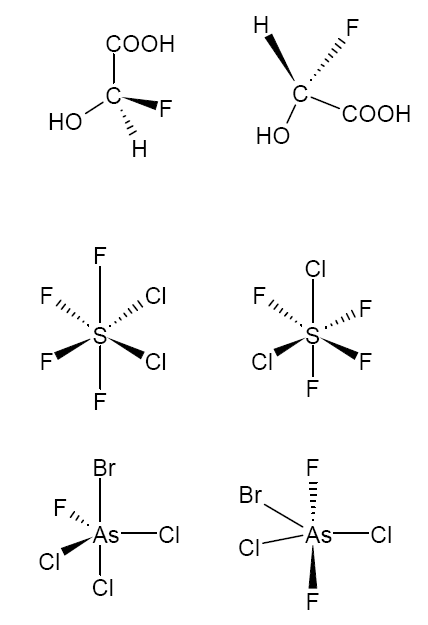
Which of the pairs of molecules below are a) enantiomers, b) stereoisomers, c) not stereoisomeric?







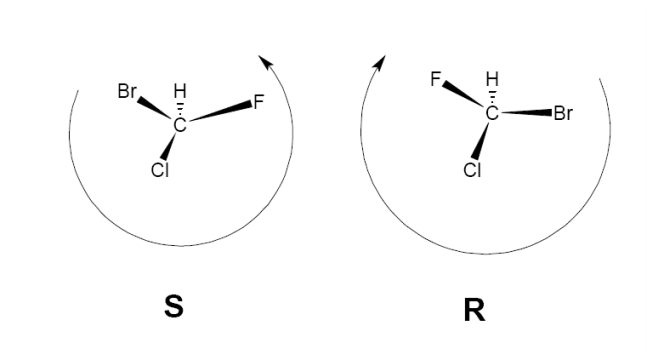
Enantiomers can be assigned a directionality of either R or S. A simplified way that these labels are assigned for carbon derivatives is as follows:

-Point the lowest molecular weight substituant away from you.

- Order the three others according to molecular weight. If the molecular weight decreases in a clockwise direction, then the molecule can be assigned R, whereas if the molecular weight of the substituents decreases anticlockwise, then S. It should be noted that this last step is slightly more subtle for more complicated molecules, but is applicable in this question.

e.g.



Assign either R or S to the following two molecules:




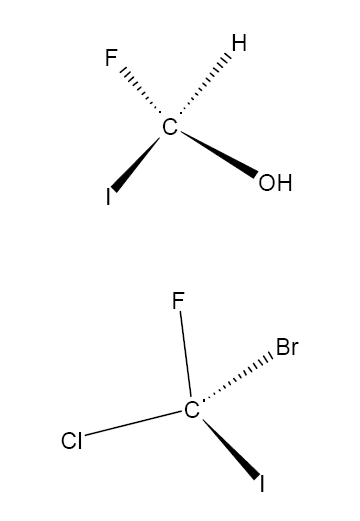
Extension: For a molecule based around a central carbon atom (as in the above two examples), what is the requirement on the substituents for there to be the possiblity of enantiomers?


[Image from: http://commons.wikimedia.org/wiki/File:Helix.png]