Euler's Buckling Formula
When you apply a steadily increasing axial load to an initially-straight strut after a while it will start to bend, and then, when a critical load $P$ is reached, it will buckle. You could try it with a matchstick.
Euler showed that at the point of buckling the strut is in a static equilibrium state: like a ball balanced at the top of a slope where the slightest push will cause it to roll down. At each point along the beam the moment due to the bending stiffness and the moment due to the axial force being applied are perfectly in balance, and if you increase the load by just a tiny bit it will break.
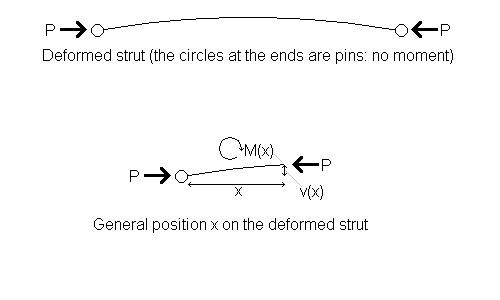
By considering a general position $x$ on the deformed strut, you can derive Euler's basic formula for $P$ by constructing and solving a second order differential equation.
You need to know two new engineering formulae: The moment due to stiffness is $M = B \kappa$, where $B$ is bending stiffness (a property of the beam) and $\kappa$ is curvature. You also need to know that we can approximate $\kappa$ as $-\frac{d^2v}{dx^2}$, where $v$ is displacement in the direction perpendicular to the initial direction of the beam (see Beam Me Up for a derivation of this).
You may also like
Lunar Leaper
Gravity on the Moon is about 1/6th that on the Earth. A pole-vaulter 2 metres tall can clear a 5 metres pole on the Earth. How high a pole could he clear on the Moon?
Wobbler
A cone is glued to a hemisphere. When you place it on a table in what position does it come to rest?
Bridge Builder
In this short problem we investigate the tensions and compressions in a framework made from springs and ropes.