Impedance Can Be Complex!
An AC generator of rms voltage E is connected in series with two reactive impedances,
$Z_1$ and $Z_2$, as shown below:
$\theta$ is the argument of $Z_1$ and $\phi$ is the argument of $Z_2$.
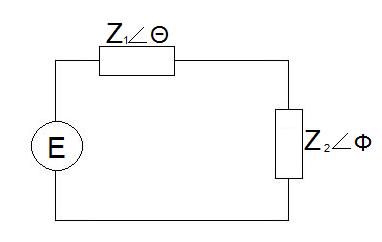
Find the power dissipated in $Z_2$
If the phase of $Z_2$ ($\phi$) is fixed whilst allowing the magnitude to vary, find the relationship between $Z_1$ and $Z_2$ when we achieve maximum power transfer to $Z_2$.
You may also like
Roots and Coefficients
If xyz = 1 and x+y+z =1/x + 1/y + 1/z show that at least one of these numbers must be 1. Now for the complexity! When are the other numbers real and when are they complex?
Target Six
Show that x = 1 is a solution of the equation x^(3/2) - 8x^(-3/2) = 7 and find all other solutions.
8 Methods for Three by One
This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?