Skip over navigation
Ben Twigger and Tom Ruffett from Ousedale School, Milton Keynes set up a spreadsheet which shows that
$$1^n + 19^n + 20^n + 51^n + 57^n + 80^n + 82^n = 2^n + 12^n + 31^n + 40^n + 69^n + 71^n + 85^n$$
for values of $n$ from $n = 1$ to $n = 6$ but the two expressions are not equal for $n = 7$ or $n = 8$. Ben and Tom found this hard to believe themselves even though they had the evidence from their own work. The two columns headed 'sum' give the totals of the expressions on the left hand side and the right hand side for each value of $n$. The column headed 'Difference' gives the differences between these two totals for each value of $n$. Notice that the difference is 0 for $n = 1, 2, 3, 4, 5, 6$ showing that the expressions are equal for these values of $n$ and the difference is not zero for $n=7$ or $n=8$ showing that these expressions are not equal for these values of $n$.
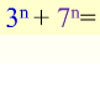
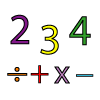
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Like Powers
Age 11 to 14
Challenge Level 





- Problem
- Student Solutions
Ben Twigger and Tom Ruffett from Ousedale School, Milton Keynes set up a spreadsheet which shows that
$$1^n + 19^n + 20^n + 51^n + 57^n + 80^n + 82^n = 2^n + 12^n + 31^n + 40^n + 69^n + 71^n + 85^n$$
for values of $n$ from $n = 1$ to $n = 6$ but the two expressions are not equal for $n = 7$ or $n = 8$. Ben and Tom found this hard to believe themselves even though they had the evidence from their own work. The two columns headed 'sum' give the totals of the expressions on the left hand side and the right hand side for each value of $n$. The column headed 'Difference' gives the differences between these two totals for each value of $n$. Notice that the difference is 0 for $n = 1, 2, 3, 4, 5, 6$ showing that the expressions are equal for these values of $n$ and the difference is not zero for $n=7$ or $n=8$ showing that these expressions are not equal for these values of $n$.
| n | 1 | 19 | 20 | 51 | 57 | 80 | 82 | sum | Difference |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 19 | 20 | 51 | 57 | 80 | 82 | 310 | 0 |
| 2 | 1 | 361 | 400 | 2601 | 3249 | 6400 | 6724 | 19736 | 0 |
| 3 | 1 | 6859 | 8000 | 132651 | 185193 | 512000 | 551368 | 1396072 | 0 |
| 4 | 1 | 130321 | 160000 | 6765201 | 10556001 | 40960000 | 45212176 | 103783700 | 0 |
| 5 | 1 | 2476099 | 3200000 | 345025251 | 601692057 | 3276800000 | 3707398432 | 7936591840 | 0 |
| 6 | 1 | 47045881 | 64000000 | 17596287801 | 34296447249 | 2.62E+11 | 3.04E+11 | 6.18E+11 | 0 |
| 7 | 1 | 893871739 | 1280000000 | 8.97E+11 | 1.95E+12 | 2.10E+13 | 2.49E+13 | 4.88E+13 | 36021585600 |
| 8 | 1 | 16983563041 | 25600000000 | 4.58E+13 | 1.11E+14 | 1.68E+15 | 2.04E+15 | 3.88E+15 | 1.28E+13 |
| n | 2 | 12 | 31 | 40 | 69 | 71 | 85 | sum | |
| 1 | 2 | 12 | 31 | 40 | 69 | 71 | 85 | 310 | |
| 2 | 4 | 144 | 961 | 1600 | 4761 | 5041 | 7225 | 19736 | |
| 3 | 8 | 1728 | 29791 | 64000 | 328509 | 357911 | 614125 | 1396072 | |
| 4 | 16 | 20736 | 923521 | 2560000 | 22667121 | 25411681 | 52200625 | 103783700 | |
| 5 | 32 | 248832 | 28629151 | 102400000 | 1564031349 | 1804229351 | 4437053125 | 7936591840 | |
| 6 | 64 | 2985984 | 887503681 | 4096000000 | 1.08E+11 | 1.28E+11 | 3.77E+11 | 6.18E+11 | |
| 7 | 128 | 35831808 | 27512614111 | 1.64E+11 | 7.45E+12 | 9.10E+12 | 3.21E+13 | 4.88E+13 | |
| 8 | 256 | 429981696 | 8.53E+11 | 6.55E+12 | 5.14E+14 | 6.46E+14 | 2.72E+15 | 3.89E+15 | |
You may also like
Power Crazy
What can you say about the values of n that make $7^n + 3^n$ a multiple of 10? Are there other pairs of integers between 1 and 10 which have similar properties?
Largest Number
What is the largest number you can make using the three digits 2, 3 and 4 in any way you like, using any operations you like? You can only use each digit once.

