Skip over navigation
In the diagram below, triangle $ABC$ represents the garden, $CD$ represents the fence and $E$ is the foot of the perpendicular from $D$ to $AC$.
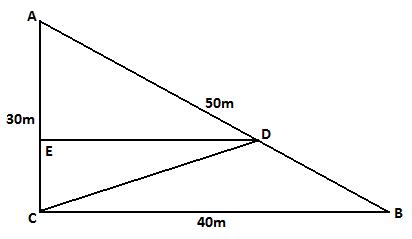
The two sections of the garden have the same perimeter so $AD$ is $10$m longer than $DB$. Hence $AD=30$m and $DB=20$m.
Triangles $AED$ and $ACB$ are similar so $\frac{AE}{AC}=\frac{AD}{AB}=\frac{30}{50}$. Hence $AE=\frac{3}{5}\times 30$m $=18$m. So $EC=(30-18)$m $=12$m.
Also $\frac{ED}{CB}=\frac{AD}{AB}=\frac{30}{50}$. Hence $ED=\frac{3}{5}\times 40$m $=24$m.
Finally, by Pythagoras: $CD^2=EC^2+ED^2=(12^2+24^2)$m$^2=5\times12^2$m$^2$. So the length of the fence is $12\sqrt{5}$m.
Garden Fence
Age 14 to 16
ShortChallenge Level 
In the diagram below, triangle $ABC$ represents the garden, $CD$ represents the fence and $E$ is the foot of the perpendicular from $D$ to $AC$.
The two sections of the garden have the same perimeter so $AD$ is $10$m longer than $DB$. Hence $AD=30$m and $DB=20$m.
Triangles $AED$ and $ACB$ are similar so $\frac{AE}{AC}=\frac{AD}{AB}=\frac{30}{50}$. Hence $AE=\frac{3}{5}\times 30$m $=18$m. So $EC=(30-18)$m $=12$m.
Also $\frac{ED}{CB}=\frac{AD}{AB}=\frac{30}{50}$. Hence $ED=\frac{3}{5}\times 40$m $=24$m.
Finally, by Pythagoras: $CD^2=EC^2+ED^2=(12^2+24^2)$m$^2=5\times12^2$m$^2$. So the length of the fence is $12\sqrt{5}$m.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...
Contact
A circular plate rolls in contact with the sides of a rectangular tray. How much of its circumference comes into contact with the sides of the tray when it rolls around one circuit?