Reflector ! Rotcelfer

Reflector ! Rotcelfer

An activity for two, three or four pupils working together.

 

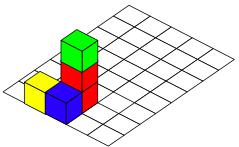
Well, that's three photos of three different ways of putting some blocks together. But there's a mirror behind the black strip. In the mirror you can see the reflections.

Now here are some more pictures but only the reflection is shown and you have to place blocks that will make this reflection.

 

 

 

 

 

There's a grid to help you.

Here's another for you to try.

 

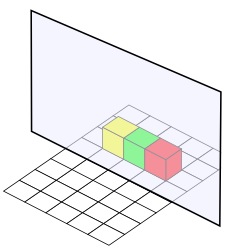
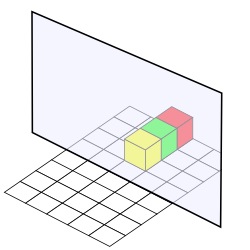
Now here are two that will probably need more careful thinking.

 

 

 

 

 

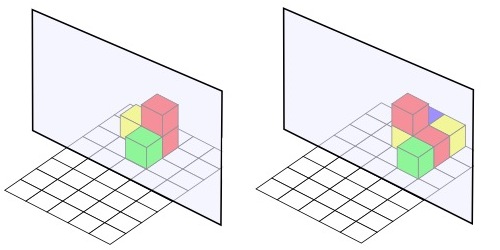
So, one of your group makes a model, maybe something like this;

 

 

 

 

 

 

Others in the group now have to make the image that would be seen in the mirror.
You therefore make it like the one behind the mirror, as here;
 

 

Now it's over to you, remember to use a variety of colours in your models and the reflections must show the correct colour positions.

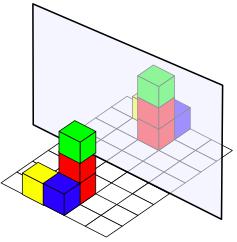
Why do this problem?

Possible approach

Show one of the images of the reflected cubes to the class. Discuss what the picture is showing us - we can see a mirror and a reflection, but we don't know what the original arrangement was. What could it have been? Encourage pupils to explore this in pairs, giving reasons for their ideas. Choose a child to describe their thinking to the class, drawing or making the arrangement of cubes and explaining how they know where the cubes should be. 

Hand out the other three pictures (all four pictures can be downloaded as a word or pdf file) In groups, pupils could make the reflection and the original arrangements for each one with coloured cubes, putting these cubes on large squared paper with a mirror in between the two arrangements. Once a group has completed all three arrangements, they can explain their solutions to an adult before moving on to the next step of making their own arrangements. Each child then takes it in turns to make a cube arrangement on one side of the mirror, with the rest of the group working together to make the reflection on the other side.

Key questions

How can you decide what goes where?
How many squares are there between that block and the mirror line?
Which cube is next to that cube in the reflection?
Tell me about your answer.

Possible extension

This activity can easily be extended by adding to the number of blocks used by one of the group when the others are trying to produce the reflection.

Possible support

Some children might benefit from having the original arrangements made for them out of cubes, rather than starting from the pictures.